その6 A*経路探索アルゴリズム
~ 経路探索の基礎の一つ ~
① 経路探索
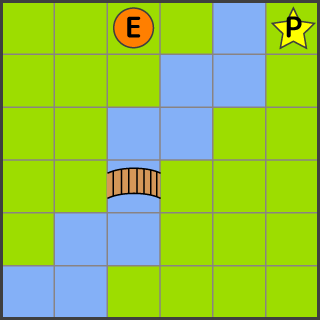
ゲームには「自動的にどこかの目的地に向かう」というシチュエーションが沢山あります。例えば敵が自分を見つけて追いかけてくる(自分が目的地)とか、ゴッドゲームなどで特定のキャラクタにある建物に向かって進めと命令した場合などです。この時、その目的地に向かって真っすぐ進めるなら簡単なのですが、障害物があったり川が流れていて橋の上しか移動できないなど移動に制約や障害が起こる事も良くあります:
緑色の所が平原、青い所が川だとします。また敵(E)はプレイヤーに接近して攻撃する必要があるとします。もし動き方として「プレイヤーの方へ常に向かうアルゴリズム」で移動するとしたら、右に移動しますがすぐ川縁にはまってしまいます。これではプレイヤーの脅威にはなりませんし「敵は真っすぐにしか向かってこない」と動きを見抜いてしまい、ゲームが単調になってしまいます。ゲームに緊張感を与えるためにも、敵Eには何とか橋を渡ってプレイヤーを追い詰めて欲しいわけです。
そこで敵Eの移動できる範囲を前もって調べる事にします。斜め移動は無しで上下左右のみの移動とすると、初期位置では左右と下に移動が可能です。その移動数をマスに描いておきます:
次に1マス移動した先からさらに移動できる範囲を調べます。左と下の「1」から先に進めますね。移動量は「2」となります:
この作業を順次続けていくと…、
プレイヤーのいる所まで11手でたどり着ける事がわかりました。ここからプレイヤーまでのルートを得るには、プレイヤー側から数字を逆にたどっていきます:
このように自分が進める方向を片っ端から検索してステップ数を記録していけば、上のようにちゃんと川を回避して橋を渡り目的地まで最短手数で辿り着けます。これで晴れて敵はプレイヤーの脅威にランクアップ(^-^)。ちなみにこの経路探索は「ダイクストラ法」という探索方法の特殊バージョンになっています。
この方法は堅実な方法なのですが、兎に角探索手数が多くなるのがネックです。上のサイズ位ならさほどではありませんが、もっと広いマップになると面積に比例して手数が増えていきます。何とか手数を減らす方法は無い物でしょうか?上の探索は言ってみれば「かくれんぼの鬼」のような探索方法です。相手の居場所がわからないのですからしらみつぶしに探すしかありません。でも上の場合はプレイヤーの位置はしっかり意識出来ているはずです。ですから橋を渡った後は下側など検索せず、真っすぐプレイヤーの方へ向かえば手数を削れますよね。この発想(目的地に向かう感覚)を利用してより早く目的地へたどり着こうとする経路探索方法が今回紹介する「A*アルゴリズム」です(読み方は「エースター」)
② ヒューリスティック関数で目的の方を優先的に探索
A*アルゴリズムでは「目的地に近付く最短距離」を表現する必要があります。上のような単純な矩形領域であれば、川などの障害物を無視してプレイヤーの方へ実直に向かうルートが最短です:
今敵Eの位置は(3,6)で、プレイヤーの位置は(6,6)です。ここから目的地の方に近付く最短距離は、お互いの要素を引き算した絶対値を足し合わせて|3 - 6| + |6 - 6| = 3と計算出来ます。この「お互いの要素を引き算した絶対値を足し合わせる」という最短距離を求める関数を「ヒューリスティック関数」と言います。ヒューリスティックというのは「発見的な(heuristic)」という意味です。
このヒューリスティック関数は今いる位置から目的地までの手数の推定値になります。勿論途中に障害物があると推定値は外れてしまいますが、鬼ごっこで逃げている人の方に走った方が近道であるのと一緒で、少なくとも闇雲に検索するよりは目的地に近付く確率は高くなるだろうと期待出来ます。
ではまずシンプルな状況で具体的に探索してみましょう:
上の敵Eの位置から1歩進んだ位置のステップ数を黒い数字で示しています。各「1」の位置からヒューリスティック関数を使ってプレイヤーまでの最短距離推定値を求めます。その値を紫の数字で示しました。黒い数字は確実なステップ数なのに対し紫の数字はそこから目的地までの推定数です。よってこれらを足した値は初期位置から目的地までの推定ステップ数とみなす事が出来ます。その合計ステップ数を青い数字で示しました。ここから上方向と右方向がその他よりもより目的地に近そうだと分かります。
そこでその「より近そうな所」から検索します。2ステップ目は次のようになります:
先ほどと全く同様に確実なステップ数(黒数字)とヒューリスティックな推定値(紫数字)を足して推定ステップ数(青数字)を算出します。最短で7ステップでたどり着けそうな箇所が3点あると分かりました。この3点について同様の作業を繰り返していくと、プレイヤーの方に向かうように優先的に探索が進んでいく事が感覚的にも分かりますよね。
上のような障害物が無い矩形領域であればこのヒューリスティック関数を使う事で確実に最短ルートを検索できます。これはヒューリスティック関数が完璧に最短数を計算できているためです。このような関数を「パーフェクトヒューリスティック関数」といいます。ただそういうのは稀でして、一般的にはヒューリスティック関数はあくまでも推定値を算出するに過ぎません。
③ 障害物があっても大丈夫?
障害物があるフィールドに対してA*アルゴリズムで経路探索してみましょう:
先ほどと同様に1ステップ目の位置に対してヒューリスティックな推定値を求めて足し算すると、上方向が最短と出ました。しかし、上方向はそれ以上先に進む道がありません。この場合、次の候補である推定9ステップのマスを採用します。2ステップ目に進みましょう:
左の9はもう手詰まりなので、どうやら右の方が近いようです。さらに進めていくと…、
このように壁を出てからはプレイヤーの方へガンガン進んでいき、最短経路を無事発見出来ました。このようにA*アルゴリズムは障害物があってもちゃんと迂回して目的地にたどり着けます。
④ 斜め移動を許可する場合
矩形フィールドで斜め移動を許可する場合、ヒューリスティック関数を変更する必要があります。斜め移動が横や縦移動と同じコストだとすると、推定最短距離はプレイヤーまでの縦もしくは横で差が大きい方になります:
1歩として進める方向が上下左右斜めになるので検索する場所は増えますが、③までと同じ方法で斜めも考慮した最短移動経路を検索可能です。もちろん回避行動もバッチリ行えます。
⑤ 不均一コストフィールドの場合
フィールドによっては進む事は出来るけどもコストが高いという場所もあるでしょう。例えば沼地のような所は入ると足が遅くなってしまいます。その場合、ヒューリスティック関数はそのままでも大丈夫ですが、1ステップごとのコスト計算が変わってきます。沼に入らない方が早いかもしれませんし、障害物の状況によっては「沼に入った方が早い」という結果になる事もあります。そういうのもA*はちゃんと判断できます。実際にそういう例をやってみましょう:
茶色の所が沼で2ステップ余計にかかるとしましょう。1ステップ目の推定ステップ数で見ると右側が早そうなので、沼は避けて右側をチェックしていく事になります。すると、
推定コストが増えてしまいました。壁のせいでプレイヤー方向に近づけず遠回りになってしまったからです。このように進むと推定コストが増加する事はもちろんあります。その場合、現在検査中のセルの中で一番推定コストが小さい物を優先的にチェックします。と言っても上の場合は皆「6」なので、さらに右側に伸長してみます:
さらに推定コストが増加して8になってしまいました。この段階で右への伸長はストップ、もっと推定コストの低いセルにスイッチします。どの「6」からでも構いませんが、結局は沼セルのから上方向に抜ける道が唯一先へ続きそうな道となります。最後まで検索を進めると、
このように推定ステップ数が6を上回る事はなく、そのままの順路でプレイヤーまで行きつきました。「一番小さい推定コストセルから進んでいく」という方針を貫けば、不均一コストなフィールド(遠回りがあるフィールド)でも最短の道を検索できます。
⑥ セルじゃないフィールドだとどうする?
フィールドが常に上のようなセル構造になっている訳ではありません。アナログレバーで自由な方向に移動できるオープンフィールドの場合「ステップ数」という概念が無くなってしまいます。そういう状況でA*アルゴリズムを応用するとした場合、セルの代わりに「目印(ノード)」を設けます。そして目印同士を線で結んで道筋とします:
セルの時と違い敵もプレイヤーも目印の上にいない事が大半です。そこで敵味方共に近場の目印とその場限りの結合をしておきます。この状態で第1ステップとして敵Eと結合している目印まで移動したとして、その距離を求めます:
黒数字がその距離です。これは確実に求まる値になります。紫の値はヒューリスティック関数による距離です。これはその地点と目的地であるプレイヤーまでの実距離となります。先と同じようにそれらを足すとEからPまでの推定距離となります。この段階では距離9が一番近い(赤丸の地点)と出ましたので、その地点から2ステップ目を算出します。
2ステップ目は一番左の点と橋の手前の点、そして敵Eの右下にある点の3つとリンクしています。それぞれの推定距離は次の通り:
赤文字でS2と書かれている方が2ステップ目での距離、S1が1ステップ目での距離です。同じ地点に辿り着いた時に、どの点も1ステップ目の推定値の方が値が小さいですよね。これは1ステップ目で最短だと思っていた赤丸で囲った地点が実は遠回りだった事を意味しています。よって赤丸の点は「捨て点」となり、1ステップ目での次の最小推定距離である「11」に白羽の矢が立つことになります。
距離11の2地点からリンクする各地点での推定距離を同様に算出するとこうなりました:
S1よりS2の方が勝っている点はありません。ただ1点橋を渡った点が新規として他のどの点よりも推定距離が短い結果になっています。つまりこれが2ステップ目の最有力候補に躍り出た事になります。ここから3ステップ目をさらに探索です。
3ステップ目は3つの点及びプレイヤーとリンクしています。この段階で目的地に到達としてもほぼ問題ありませんが、一応他の点の推定距離も算出して比較しておきましょう:
プレイヤーの所がやはり一番推定距離が短くなりました。後は確定した各点を逆にたどって経路(赤い線)を確定し、敵Eをこの経路沿いにふわ~っと移動させればプレイヤーの所までたどり着きます。
⑦ 経路探索をするタイミング
さて、リアルタイムに動くアクションゲームなどでこれまでの経路探索を使用する事を考えてみます。あるフレームでプレイヤーの位置を見て最短経路をA*で検索出来たとしましょう。しかし、その次のフレームでその経路はもはや最短では無くなるかもしれません。なぜなら、目標点であるプレイヤーが動いてしまうからです。とすると、そのフレームでまたA*で経路を計算し直す必要があります。でも次のフレームでそれは使えなくなる…。ターン性の、プレイヤーや目的地が動かない前提ならまだ良いとして、リアルタイムで目標点が動き回るゲームでは1フレーム分動くためだけに結構な負荷があるA*を都度再計算しなければなりません。これは…何か本末転倒な状態です。
私たちの普段の行動を振り返ってみましょう。
私たちは、道を歩く時に脳みそをフル回転して経路を毎回考えているでしょうか?多分そんな事は無くて、曲がり角とか交差点とか信号機の所など「要所」でちらっと経路を考えます。相手が動いているとしても毎度相手との距離を考え続けるのではなくて、最初に決めた経路を暫く歩いてみて「このまま進むか考え直すか」と断続的な判断をします。これと同じ事をリアルタイムに動くアクションゲームで適用すれば良いんです。
敵がプレイヤーを発見した時、最初のA*アルゴリズムを走らせます。経路が決まったらある程度の時間その経路でプレイヤーに近付きます。数秒程度の短時間であればプレイヤーの移動距離はそれ程大きくはありません。これは最初の経路通りに進むと高い確率でプレイヤーに近付ける事を意味しています。ある時間が経過したら、もう一度A*アルゴリズムを走らせ直します。今までと同じ経路になるかもしれませんし、プレイヤーの移動位置によっては新しい経路になるかもしれません。少なくとも地続きになっているのであれば経路は確定しますので、さらにプレイヤーに近付く事が可能になります。これを繰り返していくとホーミング弾のように徐々にプレイヤーに近付く動きになります。
最後の方はA*を使わずにプレイヤーに直接向かっていってもほぼ問題無くなります(間にある障害物はレイを飛ばすなどしてチェックします)。このように間引き作戦にすれば、大きく負荷を軽減出来ます。
という事で、この章ではA*アルゴリズムについて見てきました。経路探索はゲームの面白さの根幹を握る部分でもあり、単純にA*を使うだけでは足りない事もありますが、これをきっかけに色々な経路探索を組み合わせられるようになれば「らしさ」がぐんとアップする事間違いなしです(^-^)