2D徴撍曇
偦偺10 慄暘偲慄暘偺徴撍
丂2D偺慄暘偲慄暘偺岎揰傪媮傔傞栤戣偼怓乆側嬊柺偱弌偰偒傑偡丅捈慄摨巑偲堘偄丄慄暘偼抂偑愗傟偰偄傑偡偺偱偦偺暘偺張棟偑昁梫偵側傝傑偡偑丄嵟廔揑側傾儖僑儕僘儉偼嬌傔偰偡偭偒傝偱偡丅
嘆 慄暘摨巑偺徴撍敾掕
丂慄暘偺昞尰偼2偮偺抂揰丄傕偟偔偼巒揰偲儀僋僩儖偱昞偡偺偑晛捠偱偡丅傛傝嬶懱揑側忣曬傪帩偭偰偄傞偺偼巒揰偲儀僋僩儖偺昞尰側偺偱丄偙偙偱傕偦傟傪巊偄傑偡丅
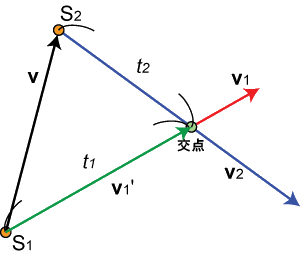
丂巒揰傪S丄廔揰偵岦偗偨儀僋僩儖傪v偲偟傑偡丅偙偺帪2偮偺慄暘傪堷偒怢偽偟偨捈慄偼岎嵎偡傞偐暲峴偐偺偳偪傜偐偱偡丅暯峴偺敾掕偼娙扨偱丄2偮偺慄暘偺曽岦儀僋僩儖v1偲v2偺奜愊傪庢偭偰0偵側偭偨傜暯峴偱偡丅暯峴偱側偄応崌偼岎揰偑1偮掕傑傝傑偡丅2捈慄偺岎揰偼師偺傛偆偵峫偊傑偡丗
丂S1偐傜岎揰傊怢偽偟偨儀僋僩儖乮v1'乯偼儀僋僩儖v偲t2丒v2偺崌惉儀僋僩儖偱偡丅偮傑傝V1' = v + t2 * v2丅偙偺崌惉儀僋僩儖偼儀僋僩儖v1偲暯峴偱偡丅偮傑傝奜愊偑0丅偙偙偐傜丄
偲側傝傑偡丅奜愊偼2峴栚偺傛偆偵暘夝偱偒傞偺偱曋棙偱偡丅傑偨奜愊偺妡偗傞弴彉傪斀懳偵偡傞偲晞崋傕斀懳偵側傞偨傔嵟屻偺2峴偑摫偗傑偡丅偙偺t2偐傜岎揰偺嵗昗偼丄
偲捈偪偵媮傑傝傑偡丅
丂偙傟偲慡偔摨條偺峫偊偱t1傕媮傑傝傑偡丅t1偺応崌乮S1-S2)=-v偲t1v1偺崌惉儀僋僩儖偲v2偑暯峴偵側傞乮奜愊偑0乯惈幙傪棙梡偟偰丄
偲側傝傑偡丅奜愊偡傞儀僋僩儖偺偆偪堦曽傪斀懳曽岦偵偡傞偲晞崋偑斀懳偵側傞惈幙傪棙梡偡傞偲嵟屻偺2峴偑摫偗傑偡丅
丂埲忋偐傜丄t1媦傃t2傪媮傔傞偵偼儀僋僩儖v乮=S2-S1乯丄Cross(v1,v2)丄Cross(v,v1)偦偟偰Cross(v,v2)偑偁傟偽椙偄偩偗偩偲傢偐傝傑偡丅
丂t1丄t2偑傢偐傞偲丄慄暘偺岎嵎傕捈偪偵傢偐傝傑偡丅偡側傢偪丄0亝t1亝1偐偮0亝t2亝1側傜偽丄2偮偺慄暘偼岎嵎偟偰偄傑偡丅
嘇 慄暘徴撍敾掕娭悢
丂慄暘摨巑偺徴撍傪敾掕偡傞娭悢傪岞奐偟傑偡丅巊偄曽偼帄偭偰娙扨側偺偱偛帺桼偵偍巊偄壓偝偄丗
慄暘徴撍敾掕娭悢 // 慄暘峔憿懱
struct Segment {
D3DXVECTOR2 s; // 巒揰
D3DXVECTOR2 v; // 曽岦儀僋僩儖乮慄暘偺挿偝傕扴偆偺偱惓婯壔偟側偄傛偆偵両乯
};
// 2D儀僋僩儖偺奜愊
float D3DXVec2Cross( D3DXVECTOR2* v1, D3DXVECTOR2* v2 ) {
return v1->x * v2->y - v1->y * v2->x;
}
// 慄暘偺徴撍
bool ColSegments(
Segment &seg1, // 慄暘1
Segment &seg2, // 慄暘2
float* outT1 = 0, // 慄暘1偺撪暘斾乮弌椡乯
float* outT2 = 0, // 慄暘2偺撪暘斾乮弌椡
D3DXVECTOR2* outPos = 0 // 岎揰乮弌椡乯
) {
D3DXVECTOR2 v = seg2.s - seg1.s;
float Crs_v1_v2 = D3DXVec2Cross( &seg1.v, &seg2.v );
if ( Crs_v1_v2 == 0.0f ) {
// 暯峴忬懺
return false;
}
float Crs_v_v1 = D3DXVec2Cross( &v, &seg1.v );
float Crs_v_v2 = D3DXVec2Cross( &v, &seg2.v );
float t1 = Crs_v_v2 / Crs_v1_v2;
float t2 = Crs_v_v1 / Crs_v1_v2;
if ( outT1 )
*outT1 = Crs_v_v2 / Crs_v1_v2;
if ( outT2 )
*outT2 = Crs_v_v1 / Crs_v1_v2;
const float eps = 0.00001f;
if ( t1 + eps < 0 || t1 - eps > 1 || t2 + eps < 0 || t2 - eps > 1 ) {
// 岎嵎偟偰偄側偄
return false;
}
if( outPos )
*outPos = seg1.s + seg1.v * t1;
return true;
}
丂D3DXVECTOR2偺奜愊娭悢偼Direct3D偵梡堄偝傟偰偄側偄偨傔丄忋偱撈帺偵愝偗偰偄傑偡丅弌椡偼3偮偁傝傑偡偑丄NULL傪搉偣偽柍帇偝傟傑偡偺偱丄岎嵎敾掕偩偗抦傝偨偄応崌偼戞2堷悢傑偱搉偣偽廫暘偱偡丅岎嵎斾妑偺晹暘偵岆嵎嫋梕抣乮0.00001f乯傪帩偨偣偰偄傞偨傔丄岎嵎敾掕偼彮偟偩偗備傞偔側偭偰偄傑偡丅