2D衝突編
その12 カプセルとカプセルの衝突
2Dの衝突図形として円は非常に優秀です。中心点の座標と半径で表現でき、他の図形との衝突計算も軽いです。ただ、ゲームには生物的なキャラクタ、STGのビーム、剣など「細長い感じ」の物もかなり多い事に気が付くと思います。これらの形状を円で表現するのはさすがに難しいです。かと言って楕円は計算負荷がとんでもないので普通採用しません。そういう「ひょろ長い感じ」にぴったりで、計算負荷もとっても軽いご機嫌な衝突図形が「カプセル」です。
① カプセルは太い線分
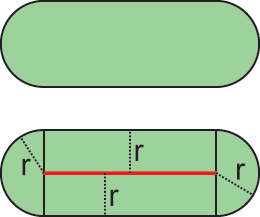
カプセルとは次のような図形です:
カプセルは線分から距離rだけ離れた点の集合です。要するに「太い線分」。この等距離に離れているという特徴は多くの場合衝突図形として優れた性質になります。
② カプセル同士の衝突は2つの線分間の距離
円は中心点から等距離にある点の集合です。なので、例えば円と点の衝突は点と円の中心点までの距離を測ればすぐに求められました。これと全く同じ発想がカプセルにも適用できます。カプセルと点との衝突は、カプセルの真ん中を走る中心線分と点との距離を調べれば良いんです。つまり、カプセルと何かとの衝突は、その何かと中心線分との距離が計算できればOKというわけです。つまりカプセル同士の衝突は「2つの線分間の距離を計算する問題」に帰着できます。
線分同士の最短距離を求める筋道は3D衝突編その27「カプセルとカプセル」にある理屈と基本的に全く一緒です。次元が一つ下がる事で簡易化できる箇所は特にありません。理屈についてはリンク先を参照頂くとしまして、3D編で示した「点と直線の距離最短」「点と線分の最短距離」「2直線の最短距離」そして「2線分の最短距離」のプログラムの2Dバージョンを以下に示します。なお、コード内で使用しているPoint2DやSegment2Dなどの基本プリミティブの定義は2D衝突編その0「2D基本プリミティブの型定義」にあります:
○ 点と直線の最短距離
点と直線の最短距離(2D版) // 点と直線の最短距離(2D版)
// p : 点
// l : 直線
// h : 点から下ろした垂線の足(戻り値)
// t :ベクトル係数(戻り値)
// 戻り値: 最短距離
float calcPointLineDist2D( const Point2D &p, const Line2D &l, Point2D &h, float &t ) {
float lenSqV = l.v.lengthSq();
t = 0.0f;
if ( lenSqV > 0.0f )
t = l.v.dot( p - l.p ) / lenSqV;
h = l.p + t * l.v;
return ( h - p ).length();
}
○ 点と線分の最短距離
点と線分の最短距離(2D版) // ∠p1p2p3は鋭角?
bool isSharpAngle( const Point2D &p1, const Point2D &p2, const Point2D &p3 ) {
return ( p1 - p2 ).dot( p3 - p2 ) >= 0.0f;
}
// 点と線分の最短距離(2D版)
// p : 点
// seg : 線分
// h : 最短距離となる端点(戻り値)
// t : 端点位置( t < 0: 始点の外, 0 <= t <= 1: 線分内, t > 1: 終点の外 )
// 戻り値: 最短距離
float calcPointSegmentDist2D( const Point2D &p, const Segment2D &seg, Point2D &h, float &t ) {
const Point2D e = seg.getEndPoint();
// 垂線の長さ、垂線の足の座標及びtを算出
float len = calcPointLineDist2D( p, seg, h, t );
if ( isSharpAngle( p, seg.p, e ) == false ) {
// 始点側の外側
h = seg.p;
return ( seg.p - p ).length();
}
else if ( isSharpAngle( p, e, seg.p ) == false ) {
// 終点側の外側
h = e;
return ( e - p ).length();
}
return len;
}
○ 2直線の最短距離
2直線の最短距離(2D版) // 2直線の最短距離(2D版)
// l1 : L1
// l2 : L2
// p1 : L1側の垂線の足(戻り値)
// p2 : L2側の垂線の足(戻り値)
// t1 : L1側のベクトル係数(戻り値)
// t2 : L2側のベクトル係数(戻り値)
// 戻り値: 最短距離
float calcLineLineDist2D( const Line2D &l1, const Line2D &l2, Point2D &p1, Point2D &p2, float &t1, float &t2 ) {
// 2直線が平行?
if ( l1.v.isParallel( l2.v ) == true ) {
// 点P11と直線L2の最短距離の問題に帰着
float len = calcPointLineDist2D( l1.p, l2, p2, t2 );
p1 = l1.p;
t1 = 0.0f;
return len;
}
// 2直線はねじれ関係
float DV1V2 = l1.v.dot( l2.v );
float DV1V1 = l1.v.lengthSq();
float DV2V2 = l2.v.lengthSq();
Vec2 P21P11 = l1.p - l2.p;
t1 = ( DV1V2 * l2.v.dot( P21P11 ) - DV2V2 * l1.v.dot( P21P11 ) ) / ( DV1V1 * DV2V2 - DV1V2 * DV1V2 );
p1 = l1.getPoint( t1 );
t2 = l2.v.dot( p1 - l2.p ) / DV2V2;
p2 = l2.getPoint( t2 );
return ( p2 - p1 ).length();
}
○ 2線分の最短距離
2線分の最短距離(2D版) // 0〜1の間にクランプ
void clamp01( float &v ) {
if ( v < 0.0f )
v = 0.0f;
else if ( v > 1.0f )
v = 1.0f;
}
// 2線分の最短距離(2D版)
// s1 : S1(線分1)
// s2 : S2(線分2)
// p1 : S1側の垂線の足(戻り値)
// p2 : S2側の垂線の足(戻り値)
// t1 : S1側のベクトル係数(戻り値)
// t2 : S2側のベクトル係数(戻り値)
// 戻り値: 最短距離
float calcSegmentSegmentDist2D( const Segment2D &s1, const Segment2D &s2, Point2D &p1, Point2D &p2, float &t1, float &t2 ) {
// S1が縮退している?
if ( s1.v.lengthSq() < _OX_EPSILON_ ) {
// S2も縮退?
if ( s2.v.lengthSq() < _OX_EPSILON_ ) {
// 点と点の距離の問題に帰着
float len = ( s2.p - s1.p ).length();
p1 = s1.p;
p2 = s2.p;
t1 = t2 = 0.0f;
return len;
}
else {
// S1の始点とS2の最短問題に帰着
float len = calcPointSegmentDist2D( s1.p, s2, p2, t2 );
p1 = s1.p;
t1 = 0.0f;
clamp01( t2 );
return len;
}
}
// S2が縮退している?
else if ( s2.v.lengthSq() < _OX_EPSILON_ ) {
// S2の始点とS1の最短問題に帰着
float len = calcPointSegmentDist2D( s2.p, s1, p1, t1 );
p2 = s2.p;
clamp01( t1 );
t2 = 0.0f;
return len;
}
/* 線分同士 */
// 2線分が平行だったら垂線の端点の一つをP1に仮決定
if ( s1.v.isParallel( s2.v ) == true ) {
t1 = 0.0f;
p1 = s1.p;
float len = calcPointSegmentDist2D( s1.p, s2, p2, t2 );
if ( 0.0f <= t2 && t2 <= 1.0f )
return len;
}
else {
// 線分はねじれの関係
// 2直線間の最短距離を求めて仮のt1,t2を求める
float len = calcLineLineDist2D( s1, s2, p1, p2, t1, t2 );
if (
0.0f <= t1 && t1 <= 1.0f &&
0.0f <= t2 && t2 <= 1.0f
) {
return len;
}
}
// 垂線の足が外にある事が判明
// S1側のt1を0〜1の間にクランプして垂線を降ろす
clamp01( t1 );
p1 = s1.getPoint( t1 );
float len = calcPointSegmentDist2D( p1, s2, p2, t2 );
if ( 0.0f <= t2 && t2 <= 1.0f )
return len;
// S2側が外だったのでS2側をクランプ、S1に垂線を降ろす
clamp01( t2 );
p2 = s2.getPoint( t2 );
len = calcPointSegmentDist2D( p2, s1, p1, t1 );
if ( 0.0f <= t1 && t1 <= 1.0f )
return len;
// 双方の端点が最短と判明
clamp01( t1 );
p1 = s1.getPoint( t1 );
return ( p2 - p1 ).length();
}
○ カプセル同士の衝突判定
カプセル同士の衝突判定(2D版) // カプセル同士の衝突判定(2D版)
// c1 : S1(線分1)
// c2 : S2(線分2)
// 戻り値: 衝突していたらtrue
bool colCapsuleCapsule2D( const Capsule2D &c1, const Capsule2D &c2 ) {
Point2D p1, p2;
float t1, t2;
float d = calcSegmentSegmentDist2D( c1.s, c2.s, p1, p2, t1, t2 );
return ( d <= c1.r + c2.r );
}
カプセル同士の衝突は上のコードにあるように2つの線分間の最短距離が双方のカプセルの半径の合計よりも小さければ衝突したと判断出来ます。3D側があるので今回はちょっと端折りました(^-^;。