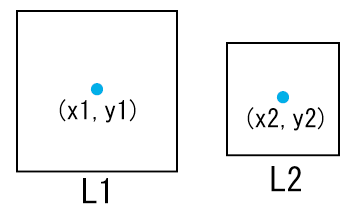
2D徴撍曇
偦偺係丂惓曽宍偲惓曽宍
丂惓曽宍偲惓曽宍偺徴撍偼丄偙傟傑偱偺復傛傝傕奿抜偵柺搢偵側傝傑偡丅偨偩偟丄惓曽宍偺曈偑X幉丄Y幉偵忢偵暯峴偱偁傞応崌偼偲偭偰傕娙扨偱偡丅
嘆 惓曽宍偺曈偑幉偵暯峴側応崌
丂惓曽宍偼侾曈偺挿偝偲婎弨偲側傞揰偑偁傟偽昞尰偱偒傑偡丅捠忢丄婎弨揰偼惓曽宍偺偳恀傫拞丄偮傑傝懳妏慄偺岎揰傪摉偰傑偡丅偙偺曽偑怓乆偲墳梡偑棙偔偨傔偱偡丅
惓曽宍1 丗 惂屼揰P1(x1, y1)丄曈偺挿偝L1
惓曽宍2 丗 惂屼揰P2(x2, y2)丄曈偺挿偝L2
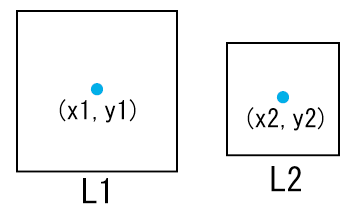
丂惓曽宍偺曈偑幉偵暯峴側応崌丄徴撍敾掕偼偝傎偳擄偟偔偼偁傝傑偣傫丅惓曽宍1偺嵍抂嵗昗偼x1-L1/2丄塃抂偼x1+L1/2偱偡偐傜丄偦偺娫偵惓曽宍2偺捀揰偑娷傑傟偰偄傞偲丄徴撍偟偰偄傞壜擻惈偑偁傝傑偡丅偝傜偵丄惓曽宍1偺壓偼y1-L1/2丄忋偼y1+L1/2偱偡偐傜丄偦偺娫偵惓曽宍2偺捀揰偑娷傑傟偰偄偨側傜偽徴撍偟偰偄傞偲敾掕偱偒傑偡丅
丂幉偵暯峴側惓曽宍偺摉偨傝敾掕傪傑偲傔傑偡丅
惓曽宍2偺捀揰 Vn(vnx, vny) , n={1,2,3,4}
(x1-L1/2)亝vnx亝(x1+L1/2)
偐偮(y1-L1/2)亝vny亝(y1+L1/2)
偑惉傝棫偰偽徴撍傪婲偙偟偰偄傞
嵟埆偺応崌16夞偺敾掕傪梫偟傑偡丅偪傚偭偲旕岠棪側婥傕偟傑偡偑丄巇曽側偄偲偙傠偱偡丅
嘇 夞揮偡傞惓曽宍偺徴撍
丂惓曽宍偑惂屼揰傪幉偲偟偰夞揮偟偩偡偲丄偦偺徴撍敾掕偼偲偨傫偵柺搢偵側傝傑偡丅傑偢丄夞揮妏搙兤傪捛壛偟傑偡丅
惓曽宍A 丗 惂屼揰PA(xa, ya)丄曈偺挿偝La丄夞揮妏搙兤a
惓曽宍B 丗 惂屼揰PB(xb, yb)丄曈偺挿偝Lb丄夞揮妏搙兤b
.gif)
恾偱偼惓曽宍A偑僾儔僗妏搙偵丄惓曽宍B偑儅僀僫僗妏搙偵夞揮偟偰偄傑偡丅徴撍傪婲偙偟偰偄傞応崌丄惓曽宍A偺拞偵惓曽宍B偺捀揰偑娷傑傟偰偄傞偼偢偱偡丅
丂崱丄惓曽宍A偺偳偙偐1揰偐傜帪寁夞傝偵捀揰偺嵗昗偑楢懕掕媊偝傟偰偄傞偲偟傑偟傚偆丅偡傞偲丄帪寁夞傝偺儀僋僩儖偑昤偗傑偡丅偝偰偙偙偱丄揰偑撪懁偵偁傞応崌丄4偮偺儀僋僩儖偐傜尒傟偽丄偦偺揰偼偄偮偱傕塃懁偵偁傞傛偆偵尒偊傑偡丅
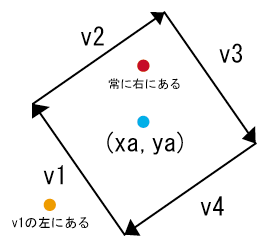
揰偑奜晹偵偁傞応崌丄椺偊偽嵍壓偺僆儗儞僕偺揰偺応崌丄v1偐傜偼嵍偵埵抲偟偰偄傑偡丅偙傟偱敾掕偡傟偽椙偄偺偱偡丅
丂儀僋僩儖偵懳偟偰揰偑嵍塃偺偳偪傜偵偁傞偺偐丠偙傟傪堦敪偱挷傋傜傟傞曋棙側墘嶼偑偁傝傑偟偨丅奜愊偱偡丅椺偊偽丄v1偺巒揰傪(vx1, vy1)丄廔揰(vx2, vy2)傪偲偟丄挷傋偨偄揰乮惓曽宍B偺捀揰乯傪P(xp, yp)偲偟傑偡丅偙偺帪奜愊丄
(vx2-vx1)*(yp-vy1) - (xp-vx1)*(vy2-vy1)
偑僾儔僗側傜偽丄揰偼儀僋僩儖v1偺嵍懁偵埵抲偟傑偡丅摨偠帠傪懠偺儀僋僩儖偵懳偟偰傕峴偊偽丄惓曽宍B偺1偮偺捀揰偵懳偟偰偺敾掕偑廔傢傝傑偡丅偙傟傪4捀揰偵偮偄偰峴偄傑偡丅
丂夞揮偺偁傞惓曽宍偺徴撍敾掕傪傑偲傔傑偡丅
惓曽宍A偺捀揰偐傜弌棃傞儀僋僩儖 VAn=(vaxn, vayn), n={1,2,3,4}
惓曽宍B偺捀揰偲惓曽宍A偺捀揰偐傜弌棃傞儀僋僩儖 VBm(vbxm, vbym), m={1,2,3,4}
VAn亊VBm偱丄1偮偺m偵懳偡偟n=1,2,3,4偡傋偰偵偍偄偰
VAn亊VBm亝0偲側傟偽徴撍傪婲偙偟偰偄傞丅
偙偺峫偊曽偼丄惓曽宍摨巑偩偗偱側偔丄帪寁夞傝偺儀僋僩儖偱峔惉偝傟偨偡傋偰偺暯柺偵偮偄偰惉傝棫偪傑偡丅偨偩丄岠棪柺偐傜偼偁傑傝傛偔偼偁傝傑偣傫丅乮偲偄偭偰傕岠棪偺椙偄曽朄偼摿偵柍偄偺偱偡偑ゥj