2D衝突編
その13 三角形と三角形の衝突
三角形同士の衝突はそれなりに需要がありそうな組み合わせなのですが、ネット上に意外と情報が少ないように見受けられます。理由はイメージよりも判定が面倒くさいためかもしれません。最も単純な凸図形同士なので衝突判定も簡単なのかなぁと思いがちですが、三角形は対称性に乏しい図形なので判定は泥臭くなってしまうんです。
単純に考えた場合、三角形の衝突には以下の衝突判定が必要です:
辺と辺の衝突は線分同士の判定なので割と面倒です。9通りの辺が全部衝突していないとしても、一方が他方を完全に包み込んでしまっている場合がある為、さらに一方の三角形の3点が他方の面内に含まれているかを判定する必要があります。そう、結構メンドクサイのです(-_-;
そこで、今回は「分離軸判定」で衝突の有無を検知してみようと思います。
① 三角形同士の分離軸
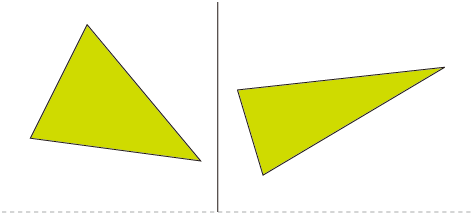
「分離軸」とは双方の図形をズバッと分断する分離線の事です:
例えば上の2つの三角形は縦に延びる直線(線分ではありません)で完全に分断できています。この直線が分離軸です。このようにもし2つの図形の間に分離軸が発見できれば、それら図形は衝突していないと判定できます。
三角形同士の場合、その辺が分離軸の候補になりえます。候補が分離軸なっているかどうかを判定するには、分離軸に垂直な線分(上の図での破線)に対して三角形を射影します:
右の三角形の一辺を分離軸候補(赤い直線)にしてみました。それに垂直な線分(破線)に両方の三角形を射影すると青い線分になります。もしこの青い線分同士に重なりが無ければ、双方の三角形は衝突していない(赤い直線が分離軸である)と判断できます。重なってしまった場合はその候補は分離軸ではないため衝突していないとは言えません。その場合は別の辺で同様にテストを行います。
双方の三角形で合わせて最大6辺分の分離軸判定を行い、それでも分離軸が見つからなかったら初めて双方の三角形は「衝突している」と判定できます。
② 三角形の外接円で1次判定
分離軸判定はあまり難しい事をしないのですが、判定までに少し手数が必要です。もし判定対象の三角形の形が変わらないのであれば、三角形の外接円を使う事で円同士の衝突判定(1次判定)によって衝突していない物を高速に判定出来ます。
三角形の外接円の求め方は色々とあるようですが、Wikipediaに従うと例えば次のようにして中心点o(外心)と半径rを算出できます:
a,b,cはそれぞれ辺の長さです。pa、pb、pcは添え字の辺の対面にある頂点の座標です。一度これらを求めておけば、三角形が移動した時はoに移動分を足し算する事で外接円の位置も移動できます。
③ 分離軸候補に垂直な直線へ三角形を投影する
分離軸の候補たる三角形の一辺に垂直な投影直線は2Dの場合簡単に定義できます。直線は「直線上の一点と方向ベクトル」で定義されます。分離軸判定に用いる投影直線は分離軸に垂直であればどこにあっても構いません。そこで、直線上の1点は「原点」にしてしまいましょう。そうすると計算の手間が少し省けます。
投影直線の方向ベクトルは三角形の一辺のベクトルから機械的に求められます:
ecは辺cの方向ベクトルです。それに垂直な方向ベクトルvcはecのXY成分をひっくり返して、片方にマイナスを付けるだけです。今直線上の一点を原点だとしているので、投影直線上の一点Lは非常に単純に、
と表現できます。sは単なる係数ですが、分離軸判定の場合この係数値がとても大切な意味を持ちます。
さて、この原点を通る投影直線に三角形の各頂点を投影させるのですが、これは内積の性質を使うと非常に簡潔に表現できます。以下の図をご覧ください:
Oは原点です。またベクトルvは正規化(長さが1)されているとします。このベクトルVに対して任意の点の座標(上の場合はベクトルでもあります)の内積を取ると、その結果は原点から投影点までの長さsになるんです。しかも、もし任意点がベクトルvと反対側の位置(鈍角になる位置)にある場合はsはマイナス値になります。こういうのを「符号付き長さ」などと言います。
分離軸判定は三角形の各頂点を投影させた時の影が重なっていない事で非衝突を判定します。sは投影点までの距離ですが、それはそのまま直線上での位置座標にもなります。つまり、各頂点に対応したsを算出し、その最小値から最大値までが影の範囲となります。影の範囲が分かれば、それが重なっていない事を示すのは非常に簡単です:
例えば上のような場合、SA,max < SB.minなので影は重なっていません。影が「重なる」条件は以下の4パターンです:
どちらかの端点がもう一方の線分に含まれているかを判定しているだけです。これらの判定で一方の影がもう一方に完全に含まれる場合も対処できます。上の4パターンのいずれにも当てはまらなかった時に影が重なっていないと判断できます。つまり「衝突していない」と判断できる分離軸が見つかったと判定される事になります。
④ 関数公開
2Dの三角形同士の衝突判定を行う関数を公開します。コード内で使用しているTriangle2Dなどの基本プリミティブの定義は2D衝突編その0「2D基本プリミティブの型定義」にあります:
三角形同士の衝突判定(2D版) // 2つの三角形の衝突判定(2D版:分離軸判定)
// t1 : 三角形1
// t2 : 三角形2
// 戻り値 : 衝突していたらtrue
bool colTriangleTriangle2D( const Triangle2D &t1, const Triangle2D &t2 ) {
const int other[] = { 1, 2, 0 };
const Triangle2D *tri[] = { &t1, &t2, &t1 };
for ( int t = 0; t < 2; ++t ) {
const Triangle2D &ta = *tri[ t ];
const Triangle2D &tb = *tri[ t + 1 ];
for ( int i = 0; i < 3; ++i ) {
// A側から分離軸の垂直線Lを算出
const Float2 &vec = ta.vec( i ).getNorm();
const Float2 sepVec( vec.y, -vec.x );
// AをLに投影
float s1min = sepVec.dot( ta.p[ i ] );
float s1max = sepVec.dot( ta.p[ other[ i ] ] );
if ( s1min > s1max ) {
float tmp = s1min;
s1min = s1max;
s1max = tmp;
}
// BをLに投影
float s2min = sepVec.dot( tb.p[ 0 ] );
float s2max = sepVec.dot( tb.p[ 1 ] );
if ( s2min > s2max ) {
float tmp = s2min;
s2min = s2max;
s2max = tmp;
}
float d3 = sepVec.dot( tb.p[ 2 ] );
if ( d3 < s2min )
s2min = d3;
else if ( d3 > s2max )
s2max = d3;
// 分離軸判定
if (
( s2min <= s1min && s1min <= s2max ) ||
( s2min <= s1max && s1max <= s2max ) ||
( s1min <= s2min && s2min <= s1max ) ||
( s1min <= s2max && s2max <= s1max )
) {
continue; // 影が重なった。まだ分からない。
}
// 分離軸発見。衝突していない。
return false;
}
}
return true; // 分離軸が無かった。衝突している。
}