3D衝突編
その22 4点が与えられた時の最小球
3D空間での球は中心点(x, y, z)と半径rで表す事ができます。未知数が4つなので、4点あれば1つの球が定まります。では、与えられた4点を囲む境界球を実際に求めてみましょう。
① 4点を通る球が最小境界球とは限らない
球は4点で一意に定まりますが、それがその4点を囲う最小の球であるとは限りません。例えばこういう場合:
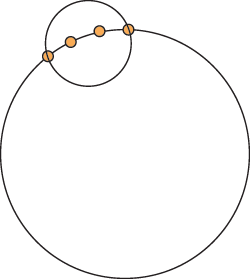
4点が綺麗に球面上に並んでいますが、それを通る境界球は見ての通り巨大です。実際は小さい方の境界球が最小になります(イメージ)。
上の小さい境界球は距離が最も離れている2点を通る球になっていますが、別のパターンもあります:
これは3点が球の赤道面上にあり、残りの1点が球の内側にあるパターンです。三角錐の底辺の三角形ポリゴンを囲む境界球がそのまま最小球になるパターンとも言えます。
最も遠い2点、もしくは三角ポリゴンを囲む境界球が最小境界球で無かった場合、初めて4点を通る球が最小境界球となります。なので結局、最小境界球を求めるには、上の三角錐の6エッジ及び4面を囲う境界球が最小境界球になっているかをチェックする必要があるわけです。
② エッジが最小境界球の場合
エッジをピッチリ囲う境界球は、そのエッジが直径になっています。なので、中心点はエッジの2等分点で、半径はエッジ間の距離の半分となります。エッジの両端をp0及びp1とすると、
2点を通る最小境界球 void calc2PointBS(
const D3DXVECTOR3 &p0,
const D3DXVECTOR3 &p1,
D3DXVECTOR3 &outP,
float &outR
) {
outP = (p0 + p1) / 2.0f;
outR = D3DXVec3Length( &(p0 - p1) ) / 2.0f;
}
となります。outPが境界球の中心点P、outRが半径rです。あるエッジに対して求めた境界球に残りの2点が含まれる場合、それで最小境界球が確定します。残り2点が含まれるかどうかは、中心点Pと残り2点との距離をそれぞれ求めて半径より小さい事を確かめれば良いだけです。
これを6つのエッジすべてでチェックします。
③ 三角ポリゴンが最小境界球の場合
どのエッジをチェックしても最小境界球にならなかった場合、今度は三角錐の面を構成する三角ポリゴンを囲う境界球と残り1点との関係をチェックします。もしその境界球の内側に残りの1点が含まれていたら、それが最小境界球になります。
三角ポリゴンを包む最小境界球はその20「三角ポリゴンを囲む最小境界球」ですでに導いていますので、そのアルゴリズムをそのまま使い回します:
3点を通る最小境界球 void calc3PointBS(
D3DXVECTOR3 p0,
D3DXVECTOR3 p1,
D3DXVECTOR3 p2,
D3DXVECTOR3 &outP,
float &outR
) {
// 鈍角三角形?
float dot0 = D3DXVec3Dot( &(p1 - p0), &(p2 - p0) );
if ( dot0 <= 0.0f ) {
outP = (p1 + p2) / 2.0f;
outR = D3DXVec3Length( &(p1 - p2) ) / 2.0f;
return;
}
float dot1 = D3DXVec3Dot( &(p0 - p1), &(p2 - p1) );
if ( dot1 <= 0.0f ) {
outP = (p0 + p2) / 2.0f;
outR = D3DXVec3Length( &(p0 - p2 ) ) / 2.0f;
return;
}
float dot2 = D3DXVec3Dot( &(p0 - p2), &(p1 - p2) );
if ( dot2 <= 0.0f ) {
outP = (p0 + p1) / 2.0f;
outR = D3DXVec3Length( &(p0 - p1) ) / 2.0f;
return;
}
// 鋭角三角形
// 3頂点から等距離にある点が中心。連立方程式を解きます。
D3DXVECTOR3 N;
D3DXVec3Cross( &N, &(p1 - p0), &(p2 - p0) );
D3DXVECTOR3 v0, v1, e0, e1;
D3DXVec3Cross(&v0, &(p2 - p1), &N );
D3DXVec3Cross(&v1, &(p2 - p0), &N );
e0 = (p2 + p1) * 0.5f;
e1 = (p2 + p0) * 0.5f;
float a = D3DXVec3Dot( &v0, &v1 );
float b = D3DXVec3Dot( &v0, &v0 );
float c = -D3DXVec3Dot( &(e1-e0), &v0 );
float d = D3DXVec3Dot( &v1, &v1 );
float e = -D3DXVec3Dot( &(e1-e0), &v1 );
float div = -a*a + b*d;
float t = (-a*c + b*e) / div;
float s = (-c*d + a*e) / div;
outP = e0 + s * v0;
outR = D3DXVec3Length( &(outP - p0) );
}
calc3PBS関数で境界球の中心点Pと半径rを求めたら、残り1点がその境界球に含まれているかをチェックします。もし含まれていたら最小境界球が確定です。
これを4面すべてについてチェックします。
④ 4点を通る球
エッジと面、それらがいずれも最小境界球ではないと判定されたら、4点を通る球が最小境界球である事が確定します。
4点を通る球の中心点Pから各点への距離はもちろん同じで、その半径はrとなります。これをどう求めるかですが、例えば次のように考えるのはどうでしょうか:
点p0,p1,p2で作られる三角ポリゴンを囲う最小境界球をすでに求めているはずなので、その中心点c0は既知です(左図)。このc0から伸びる三角形p0p1p2に垂直な線分を想定すると、この線分上のどの点PからもP0,p1p,2への距離は等しくなります。という事は、この線分のどこかにP-P3も同じ長さとなる点Pが存在するはずですよね(右図)。
よって、上の問題は「線分上で点p0及び点p3までの距離が等しくなる点Pを求める」という問題に帰着します。
点Pはc0とベクトルvを用いて、
と表せます。aは係数で、ベクトルvは標準化されているとします。点p0-P及びp3-Pの距離(の2乗)は内積を使って、
と表現できます。内積は分解できまして、上のL0やL3は、
と展開ができます。ここでL0=L3と等号で結んでしまいます。両方にDot(P,P)が入っているので、これは消えてしまいます。残ったのを整理すると、
と、欲しいaが出てきます。上でD=Dot(p0,p0)-Dot(p3,p3)です。
引数に4頂点を渡してその点を通る球を返す関数はこんな感じです:
4点を通る最小境界球 void calc4PointBS(
const D3DXVECTOR3 &p0,
const D3DXVECTOR3 &p1,
const D3DXVECTOR3 &p2,
const D3DXVECTOR3 &p3,
D3DXVECTOR3 &outP,
float &outR
) {
// 三角形p0p1p2を囲う境界球の中心点を取得
D3DXVECTOR3 c0;
float tmpR;
calc3PointBS( p0, p1, p2, c0, tmpR );
D3DXVECTOR3 v;
D3DXVec3Cross( &v, &(p1-p0), &(p2-p0) );
D3DXVec3Normalize( &v, &v );
// len(P-p0) = len(P-p3)となるPを算出
float D = D3DXVec3Dot( &p0, &p0 ) - D3DXVec3Dot( &p3, &p3 );
float a = ( -2.0f * D3DXVec3Dot( &c0, &(p0-p3) ) + D ) / ( 2.0f * D3DXVec3Dot( &v, &(p0-p3) ) );
outP = c0 + a * v;
outR = D3DXVec3Length( &(outP - p0) );
}
さ、これでツールは揃いました。
⑤ 与えられた4点を囲む最小境界球
4点を与えた時にその最小境界球を返す関数を公開します:
4点を通る最小境界球 bool checkTriangleMinimum(
D3DXVECTOR3 p0,
D3DXVECTOR3 p1,
D3DXVECTOR3 p2,
D3DXVECTOR3 other0,
D3DXVECTOR3 &outP,
float &outR
) {
calc3PointBS( p0, p1, p2, outP, outR );
if ( D3DXVec3Length( &(outP - other0) ) > outR )
return false;
return true;
}
void calc4PointMinimumBS(
D3DXVECTOR3 p0,
D3DXVECTOR3 p1,
D3DXVECTOR3 p2,
D3DXVECTOR3 p3,
D3DXVECTOR3 &outP,
float &outR
){
// 6エッジ、4三角面をチェック
if ( checkEdgeMinimum( p0, p1, p2, p3, outP, outR ) == true ) return;
if ( checkEdgeMinimum( p0, p2, p1, p3, outP, outR ) == true ) return;
if ( checkEdgeMinimum( p0, p3, p1, p2, outP, outR ) == true ) return;
if ( checkEdgeMinimum( p1, p2, p0, p3, outP, outR ) == true ) return;
if ( checkEdgeMinimum( p1, p3, p0, p2, outP, outR ) == true ) return;
if ( checkEdgeMinimum( p2, p3, p0, p1, outP, outR ) == true ) return;
if ( checkTriangleMinimum( p0, p1, p2, p3, outP, outR ) == true ) return;
if ( checkTriangleMinimum( p0, p1, p3, p2, outP, outR ) == true ) return;
if ( checkTriangleMinimum( p0, p2, p3, p1, outP, outR ) == true ) return;
if ( checkTriangleMinimum( p1, p2, p3, p0, outP, outR ) == true ) return;
// 4点を通るのが最小球
calc4PointBS( p0, p1, p2, p3, outP, outR );
}
でですね、ここから点を与えるとその最小球を自動的に計算してくれるSphere構造体を作っておきます:
最小境界球構造体 struct Sphere {
D3DXVECTOR3 p;
float r;
Sphere() : p( D3DXVECTOR3(0.0f, 0.0f, 0.0f) ), r() {}
Sphere( const D3DXVECTOR3 &p0 ) : p(p0), r() {}
Sphere( const D3DXVECTOR3 &p0, const D3DXVECTOR3 &p1 ) {
calc2PointBS( p0, p1, p, r );
}
Sphere( const D3DXVECTOR3 &p0, const D3DXVECTOR3 &p1, const D3DXVECTOR3 &p2 ) {
calc3PointBS( p0, p1, p2, p, r );
}
Sphere( const D3DXVECTOR3 &p0, const D3DXVECTOR3 &p1, const D3DXVECTOR3 &p2, const D3DXVECTOR3 &p3 ) {
calc4PointMinimumBS( p0, p1, p2, p3, p, r );
}
};