3D衝突編
その23 整数区画に飛ばしたレイが通った区画を列挙してく
例えばマインクラフトのように3Dゲームだけれども立方体が単位になっているゲームでは、置かれている物の位置が整数座標で表現されます。例えば岩の位置座標が(3,6,10)という感じです。ただ、キャラクタの移動などは整数単位という事はなくて、いつも通りの浮動小数点だったりします。そういう世界で例えばある浮動小数点座標からレイを飛ばして、置かれている物をピッキングしたいという状況を考えてみます。
① まずは2Dで考えてみよう
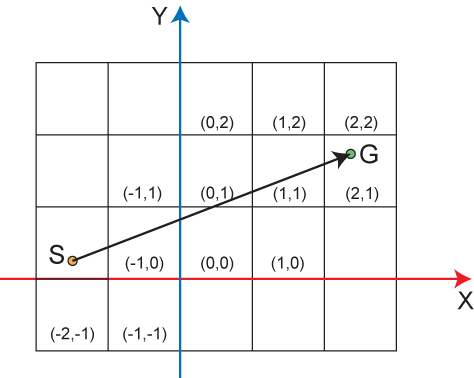
いきなり3Dで考えると頭がぐるぐるしてくるので、まずは2Dで理屈を考えてみます。整数区画の中でレイを飛ばすというのは下図のような状況です:
S地点からレイをGまで飛ばしています。この時このレイは(-2,0)、(-1,0)、(0,0)、(0,1)、(1,1)、(2,1)の区画をこの順番で通って行きます。もしこれらのどこかに対象物があれば、このレイは先の順番で一番最初に見つかる対象物と衝突する事になります。レイの長さが凄まじく長くなければ(レイが通った区画が何千もあるとか)、衝突物を先頭から線形で検索しても大したコストにはなりません。では、この順番をどうやって取得していけば良いのでしょうか?
S地点からGへ向かって進んでいくと「区画の境界」を必ずまたぐ事に気が付きます。そして上の図の場合、またいだ境界の先にある区画は必ずレイが通っています:
黄色い座標がその境界線上の交点です。これを探っていけば良さそうです。まずはS地点からスタートしてみましょうか。
② 境界交差テスト
上図のS地点付近を拡大します:
S地点は区画(-2,0)に所属しています。ちなみにこの整数座標は区画の左下の小数座標とシンクロしてます。これ、後で大事になってきますので今からルールとして定めておきます。レイは右上に伸びています。このレイがどの境界線と最初に衝突するのか?これはSが所属している区画を囲む境界線以外はありません。そして、レイは右上に向かっているので、その中でも右側の境界線(X-Side)と上の境界線(Y-Side)がその候補に挙がります。上図ではX-Sideと交差しているのがわかりますが、地点Sの位置によってはY-Sideと先に交差する事もあり得ます。
どちらが先に交差するかは、それぞれの黄色い交差点までの距離を比較すれば良さそうです。距離が近い方の黄色い点を含んでいるのが欲しい境界線です。そこで、ベクトルの性質をうまく利用してみましょう。
地点Sからスタートして右上に向かうベクトルVは、
と表せます。ここから上のレイを含む線分上の任意の点Pは、
となります。aは任意の数値で0≦a≦1の範囲ならレイ上になります。もちろん、とあるaの値の時にX-Side側の境界線上に達しますし、別のaの値でY-Side側の黄色い点の座標にもなります。上の図の場合、X-Side側のaの方がY-Side側よりも値が必ず小さくなります。これが肝です!
上の式を成分別に書き直してみましょう:
上のPx(a)は黄色い点のX座標、Py(a)はY座標になります。Sx、Vxは既知の値、と言う事は例えばX-Side上にある黄色い点の座標は、Px(a)=-1が確定していますから、
と黄色い点に達するためのaの値が求まってしまいます。同じ事はY-Sideにある黄色い点にも言えて、Py(a)=1がわかっていますので、
とY-Side側の黄色い点に達するまでのaの値もわかります。X-Side、Y-Side双方のaが求まるのですから、後はこれを比較して小さい方のaの境界線を採用すれば良いんです。
境界線を採用したら区画も決まります。採用境界線はX-Sideですから、下図のように「その境界線をまたいだ区画」は確定となります:
新しい区画の座標を求めるのは簡単で、先の場合X-Side側が採用されたのですから(-2 + 1, 0 )で求まります。Y-Side側だったらY座標側をプラス1すれば良いのは言わずもがなです。
これで判定が一巡しましたので、次の通過区画の検索に移ります。上図のように先程と同様に区画(-1,0)に対してX-Side側とY-Side側が境界線の候補です。双方の境界線上に交点が存在しています。先と全く同じようにPx(a)=0、Py(a)=1を代入して双方のaを計算、比較して小さい方の境界線を採用します。上の図だとまたX-Sideですね。なのでX-Sideをまたいだ区画(0,0)が採用となります。後は同じ事を地点Gまで繰り返すだけです:
計算を繰り返すといつかX-Side及びY-Side上の交点を求めた時に算出されるaが1.0以上(レイを越えてしまう)ので、そこで計算終了となります。
この方法ではいくつかの例外に対処しておく必要があります。例外の一つ目は交点が「角」にある場合です。X-Side、Y-Sideどちらのaも同じ値になった場合に交点は区画の角に位置してしまいます。この場合、X-Side側とY-Side側の両方が含まれる事になるでしょう。そして角を含む区画も採用となります:
このため、衝突区画を順に追ってレイとの衝突を検知する時に、上の場合は3つの区画が同時に衝突している事を知らせる必要があります。「角の時にはX-Side、Y-Side側は無視してもいいんじゃない?」という考えもありますが、そうすると角に「衝突しない点」が生まれてしまいます。角に向けて弾を発射したらX-Side、Y-Sideどちらのオブジェクトにも当たらなかったという状況が生まれてしまいますので、双方は採用した方が無難です。
例外その2はレイが軸に平衡の場合です。黄色い点の座標を求める時の式を再度見てみます:
aを計算する時に分母にレイの方向ベクトルの各成分が存在しています。これが0だとaは無限大に吹っ飛んでしまいます。数学上では問題ありませんが、プログラム上では好ましくありません。でも対処は簡単で、VxかVyが0だったらaの値をプログラム計算上で取りうる最大の値にしてしまいます。そうすれば確実に他方が採用されます。VxやVyに極小な値を入れておくというのも考えられますが、方向ベクトルを意図的に曲げると例えば地点Sが境界線上にある場合に計算誤差が出る可能性があります。
さて、このようにかなり簡単で逐次的にレイが通る区画をその順番で列挙して行けるのですが、実はこのままだと不都合が起こるパターンがあるんです。それは「方向ベクトルVの成分のいずれかがマイナス」だった場合です。
③ 方向ベクトルがマイナスの時は鏡写しで対応
下図をご覧ください:
S地点から2つのレイが飛んでいます。右側はベクトルVのX成分がプラスの場合、左側はマイナスの場合です。先程までのアルゴリズムはレイが右上(ベクトルVのX,Y成分いずれもプラス)のケースで、X-Sideは暗黙に「所属区画のX成分+1」でした。しかしX成分がマイナスの場合、上図の-X-Sideの座標は「所属区画のX成分」そのものです。この場合分けが必要になってしまうわけです。これ、些細に見えるかもしれませんが、Y成分側も同じことが言えますし、3Dに拡張するとZ成分も入ってきます。ある時はX-Sideが+1で、また別の時はZ-Sideはそのまま…みたいなのって、ちょっとやばそうですよね。
そこで、アルゴリズムは最初から見てきた「すべての成分がプラス」の物しか使いません!ではレイのベクトルの成分にマイナスが入って来たらどうするか?それは「鏡写し」にしてしまうんです。下図をご覧ください:
上の左側がレイの方向ベクトルのX成分がマイナスの場合です。区画内の数値は区画座標のX成分です。これをY軸でそっくりそのまま本当に鏡写ししたのが上の右側。方向が右上に直ったのがわかりますね。これを元の座標に戻したのが下の方の図です。区画座標の値の絶対値が変わっていて、1減ってますね。この値から元のX成分に戻すのが下図左にある「-4 = -3 - 1」という計算例です。また元のレイは(-1.2, 0.6)から始まっているのに対し、直した方のレイは(+1.2, 0.6)から始まっています。
つまり、方向ベクトルの成分がマイナスだった場合、まずその成分をプラスにしてしまいます。次に始点(終点も)の同成分の符号も反転します。後は先のアルゴリズムで区画を検索していきます。衝突が見つかった区画の座標の同成分は先の計算式で変換します。これを疑似プログラムで表現するとこうなります:
int signX = signY = 1; // 成分の符号
int adjX = adjY = 0; // 元の成分に戻す時に使用
if ( V.x < 0.0f ) {
S.x *= -1; // 始点の成分の符号を反転
V.x *= -1; // ベクトルのX成分をプラスに
signX = -1; // X成分がマイナスである印
adjX = 1; // 区画座標を算出する際に使用
}
if ( V.y < 0.0f ) {
S.y *= -1; // 始点の成分の符号を反転
V.y *= -1; // ベクトルのY成分をプラスに
signY = -1; // Y成分がマイナスである印
adjY = 1; // 区画座標を算出する際に使用
}
while(1) {
int cx, cy; // 区画座標
search( ..., &cx, &cy ); // 区画検索 (引数は省略してます)
// 区画座標を補正
cx = signX * ( cx + adjX );
cy = signY * ( cy + adjY );
}
}
こんな感じです。
④ 3Dに拡張
ここまで2Dの区画について見てきました。これは3Dに簡単に拡張できます。始点や終点が3次元になって、境界としてZ-Sideが追加されるだけです。各境界に達するまでの係数aの求め方も全く一緒です:
求めた3つのaのうち一番小さいaが直近の境界面です。
例外処理も基本的に一緒ですが、パターンがちょっと増えます。各aを(ax, ay, az)とした時、一番小さい物が2個及び3個出てくることがあります。例えばax,ayが同じ値になった場合、これは区画(立方体)のX-SideとY-Sideがクロスする辺に境界交点がある事を意味します。そのため衝突区画は3つになります:
ax, ay, azがすべて同じ値になった時、これは境界交点が立方体の角にある事を意味します。その場合は7つの区画が衝突区画になります:
⑤ レイが通った整数区画座標を列挙する関数
では以上を踏まえたレイが通った整数区画座標を列挙して返す関数を公開します:
2Dレイと衝突する2D整数領域を取得 // 2Dレイと衝突する2D整数領域を取得
// F2 : 2次元の浮動小数点座標型(x,yが定義されている事)
// I2 : 2次元の符号付き整数座標 (x,yが定義されている事)
// sp : レイの始点
// ep : レイの終点
// out : レイと衝突している2D整数領域。同時に衝突する可能性がある為配列の配列になっている
// 戻り値 : 正常終了ならtrue、エラーの場合はfalse
template< class F2, class I2 >
bool collideRayToIntRegion2D( const F2 &sp, const F2 &ep, std::vector< std::vector<I2> > &out ) {
// 初期位置が最初の衝突
std::vector<I2> res;
I2 initC;
initC.x = (int)floorf(sp.x);
initC.y = (int)floorf(sp.y);
res.push_back( initC );
out.push_back( res );
// レイベクトル算出
F2 v = ep;
v.x -= sp.x;
v.y -= sp.y;
F2 s = sp;
// レイの方向ベクトルVの成分の符号をプラス化
int signX = 1, signY = 1;
int adjX = 0, adjY = 0;
if ( v.x < 0.0f ) {
s.x *= -1.0f;
v.x *= -1;
signX = -1;
adjX = 1;
}
if ( v.y < 0.0f ) {
s.y *= -1.0f;
v.y *= -1;
signY = -1;
adjY = 1;
}
// 始点を含む領域が初期領域
I2 c;
c.x = signX * ( initC.x + adjX );
c.y = signY * ( initC.y + adjY );
if ( v.x == 0.0f && v.y == 0.0f )
return true; // レイが飛んでいないので終了
// 衝突探索
while( 1 ) {
std::vector<I2> res;
float ax = v.x != 0.0f ? (c.x + 1 - s.x) / v.x : FLT_MAX;
float ay = v.y != 0.0f ? (c.y + 1 - s.y) / v.y : FLT_MAX;
if ( ax > 1.0f && ay > 1.0f )
break; // レイを越えたのでおしまい
if ( ax < ay ) {
c.x += 1; // X-Side
} else if ( ay < ax ) {
c.y += 1; // Y-Side
} else {
c.x += 1; c.y += 1; // 角
}
I2 newC;
newC.x = signX * ( c.x + adjX );
newC.y = signY * ( c.y + adjY );
res.push_back( newC );
if ( ax == ay ) {
// 角に隣接する領域も衝突
I2 newC0, newC1;
newC0.x = signX * ( c.x + adjX );
newC0.y = signY * ( c.y - 1 + adjY );
newC1.x = signX * ( c.x - 1 + adjX );
newC1.y = signY * ( c.y + adjY );
res.push_back( newC0 );
res.push_back( newC1 );
}
out.push_back( res );
}
return true;
}
3Dレイと衝突する2D整数領域を取得 // 3Dレイと衝突する3D整数領域を取得
// F3 : 3次元の浮動小数点座標型(x,y,zが定義されている事)
// I3 : 3次元の符号付き整数座標 (x,y,zが定義されている事)
// sp : レイの始点
// ep : レイの終点
// out : レイと衝突している2D整数領域。同時に衝突する可能性がある為配列の配列になっている
// 戻り値 : 正常終了ならtrue、エラーの場合はfalse
template< class F3, class I3 >
bool collideRayToIntRegion3D( const F3 &sp, const F3 &ep, std::vector< std::vector<I3> > &out ) {
// 初期位置が最初の衝突
std::vector<I3> res;
I3 initC;
initC.x = (int)floorf( sp.x );
initC.y = (int)floorf( sp.y );
initC.y = (int)floorf( sp.z );
res.push_back( initC );
out.push_back( res );
// レイベクトル算出
F3 v = ep;
v.x -= sp.x;
v.y -= sp.y;
v.z -= sp.z;
F3 s = sp;
// レイの方向ベクトルVの成分の符号をプラス化
int signX = 1, signY = 1, signZ = 1;
int adjX = 0, adjY = 0, adjZ = 0;
if ( v.x < 0.0f ) {
s.x *= -1.0f;
v.x *= -1;
signX = -1;
adjX = 1;
}
if ( v.y < 0.0f ) {
s.y *= -1.0f;
v.y *= -1;
signY = -1;
adjY = 1;
}
if ( v.z < 0.0f ) {
s.z *= -1.0f;
v.z *= -1;
signZ = -1;
adjZ = 1;
}
// 始点を含む領域が初期領域
I3 c;
c.x = signX * ( initC.x + adjX );
c.y = signY * ( initC.y + adjY );
c.z = signZ * ( initC.z + adjZ );
if ( v.x == 0.0f && v.y == 0.0f && v.z == 0.0f )
return true; // レイが飛んでいないので終了
// 衝突探索
while( 1 ) {
std::vector<I3> res;
float ax = v.x != 0.0f ? (c.x + 1 - s.x) / v.x : FLT_MAX;
float ay = v.y != 0.0f ? (c.y + 1 - s.y) / v.y : FLT_MAX;
float az = v.z != 0.0f ? (c.z + 1 - s.z) / v.z : FLT_MAX;
if ( ax > 1.0f && ay > 1.0f && az > 1.0f )
break; // レイを越えたのでおしまい
if ( ax < ay && ax < az ) {
c.x += 1; // X-Side
} else if ( ay < ax && ay < az ) {
c.y += 1; // Y-Side
} else if ( az < ax && az < ay ) {
c.z += 1; // Z-Side
} else if ( ax == ay && ax < az ) {
// 辺に隣接する領域も衝突
I3 newC0, newC1;
newC0.x = signX * ( c.x + 1 + adjX );
newC0.y = signY * ( c.y + adjY );
newC0.z = signZ * ( c.z + adjZ );
newC1.x = signX * ( c.x + adjX );
newC1.y = signY * ( c.y + 1 + adjY );
newC1.z = signZ * ( c.z + adjZ );
res.push_back( newC0 );
res.push_back( newC1 );
c.x += 1; c.y += 1; // X-Side, Y-Side辺
} else if ( ax == az && ax < ay ) {
// 辺に隣接する領域も衝突
I3 newC0, newC1;
newC0.x = signX * ( c.x + 1 + adjX );
newC0.y = signY * ( c.y + adjY );
newC0.z = signZ * ( c.z + adjZ );
newC1.x = signX * ( c.x + adjX );
newC1.y = signY * ( c.y + adjY );
newC1.z = signZ * ( c.z + 1 + adjZ );
res.push_back( newC0 );
res.push_back( newC1 );
c.x += 1; c.z += 1; // X-Side, Z-Side辺
} else if ( ay == az && ay < ax ) {
// 辺に隣接する領域も衝突
I3 newC0, newC1;
newC0.x = signX * ( c.x + adjX );
newC0.y = signY * ( c.y + 1 + adjY );
newC0.z = signZ * ( c.z + adjZ );
newC1.x = signX * ( c.x + adjX );
newC1.y = signY * ( c.y + adjY );
newC1.z = signZ * ( c.z + 1 + adjZ );
res.push_back( newC0 );
res.push_back( newC1 );
c.y += 1; c.z += 1; // Y-Side, Z-Side辺
} else {
// 角に隣接する領域も衝突
I3 newC0, newC1, newC2, newC3, newC4, newC5;
newC0.x = signX * ( c.x + 1 + adjX ); // X
newC0.y = signY * ( c.y + adjY );
newC0.z = signZ * ( c.z + adjZ );
newC1.x = signX * ( c.x + adjX ); // Y
newC1.y = signY * ( c.y + 1 + adjY );
newC1.z = signZ * ( c.z + adjZ );
newC2.x = signX * ( c.x + adjX ); // Z
newC2.y = signY * ( c.y + adjY );
newC2.z = signZ * ( c.z + 1 + adjZ );
newC3.x = signX * ( c.x + 1 + adjX ); // XY
newC3.y = signY * ( c.y + 1 + adjY );
newC3.z = signZ * ( c.z + adjZ );
newC4.x = signX * ( c.x + 1 + adjX ); // XZ
newC4.y = signY * ( c.y + adjY );
newC4.z = signZ * ( c.z + 1 + adjZ );
newC5.x = signX * ( c.x + adjX ); // YZ
newC5.y = signY * ( c.y + 1 + adjY );
newC5.z = signZ * ( c.z + 1 + adjZ );
res.push_back( newC0 );
res.push_back( newC1 );
res.push_back( newC2 );
res.push_back( newC3 );
res.push_back( newC4 );
res.push_back( newC5 );
c.x += 1; c.y += 1; c.z += 1; // 角
}
I3 newC;
newC.x = signX * ( c.x + adjX );
newC.y = signY * ( c.y + adjY );
newC.z = signZ * ( c.z + adjZ );
res.push_back( newC );
out.push_back( res );
}
return true;
}
これらは次のように使用します:
struct Vec2 {
float x, y;
Vec2( float x = 0.0f, float y = 0.0f ): x(x), y(y) {}
};
struct Vec3 {
float x, y, z;
Vec3( float x = 0.0f, float y = 0.0f, float z = 0.0f ): x(x), y(y), z(z) {}
};
struct Vec2I {
int x, y;
Vec2I( int x = 0, int y = 0 ) : x(x), y(y) {}
};
struct Vec3I {
int x, y, z;
Vec3I( int x = 0, int y = 0, int z = 0 ) : x(x), y(y), z(z) {}
};
int _tmain(int argc, _TCHAR* argv[])
{
// 2D
Vec2 sp2( 3.5f, -2.5f ), ep2( 7.0f, 3.5f );
std::vector< std::vector<Vec2I> > collideRegions2;
collideRayToIntRegion2D< Vec2, Vec2I >( sp2, ep2, collideRegions2 );
// 3D
Vec3 sp3( 2.0f, 3.0f, -4.0f ), ep3( 5.0f, -2.0f, 2.0f );
std::vector< std::vector<Vec3I> > collideRegions3;
collideRayToIntRegion3D< Vec3, Vec3I >( sp3, ep3, collideRegions3 );
return 0;
}
結果は第3引数の整数座標の配列の配列にどばーっと返ります。この配列のが示す区画の座標を順次調べていけば、レイが最初に衝突するオブジェクトがわかります。