3D衝突編
その25 レイと無限円柱の貫通点
レイを世界に向けてブシッと飛ばした時に無限円柱と衝突しているか調べるには、円柱の軸となる直線とレイとの最短距離が円柱の半径よりも短いかどうか調べればわかります。それ自体はそれ程難しくは無いのですが、その衝突座標を求めるのは思いの外面倒くさいのです(^-^;
① 衝突点は円柱を2か所で輪切る
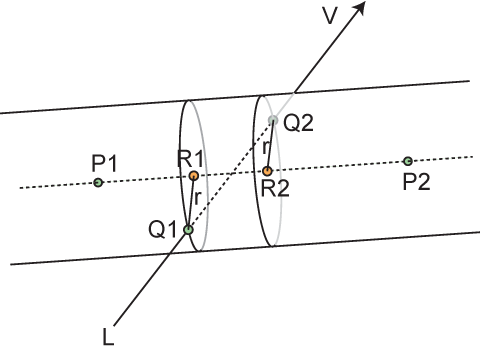
下の図をご覧ください:
無限円柱に対してレイが刺さっています。その貫通点をQ1、Q2とすると、双方の貫通点を含む輪切りとなる円がそれぞれ存在します。その円の中心座標をR1、R2とすると、その中心点から各Qへの長さは、もちろん半径rとなります。この円は円柱の中心軸に対して鉛直ですから、その円に含まれている線分R1Q1及びR2Q2もまた中心軸に対して垂直になっています。
前章と同様に、計算を少し簡単にするため、Lを原点にオフセットします。これにより円柱を定義するP1、P2もオフセットされます(上の図はオフセット後だと考えて下さい)。ここから貫通点Q1、Q2を求めてみましょう。まず、レイ上の点Qは、
と係数aと方向ベクトルVで表現出来ます。aがある値の時にQ1及びQ2になるわけです。線分R1Q1と、また線分R2Q2と円柱の中心軸はそれぞれ垂直関係にあります。ここから、
…①
と内積がゼロになる関係式①が導けます。点Rは直線P1P2上のどこかにありますから、これはP1及びP2を用いて、
と表せます。bはベクトルP1P2にかかる係数で、この値によって直線P1P2上のどの点も表現出来ます。表記を簡略化するためS=P2-P1と置きました。
もう一つ、線分R1Q1の長さはrです。ここから、
…②
も言えます。さて、今係数a及びbが未知数です。それに対して関係式は①と②の2本。ここから連立方程式が立てられそうですね。
② 係数a、bを求める
具体的な連立方程式をこれから立ててズガガっと解いていくのですが、内積を上のように表現すると記述が冗長になるため、次のようなルールで簡易表現する事にします:
内積をDとし、添え字でどの点(ベクトル)同士を掛けるか表します。では①式を展開していきましょう:
内積は通常の掛け算と似たような演算ができるのであり難いですね。ここからbをaを用いて、
…③
と表す事ができました。右辺でわざわざ分数を分解しているのは、これを②式に代入する時に少し分かりが良くなる為です。
続いて②式を展開していきましょう:
ふぅ(^-^;。さ、上の式の「b」に先程の式③を代入するのです、そして一生懸命展開するのです!
あ~大変だった…(T△T)。途中はさて置き、最終的な所はまぁそれなりにスッキリしました。最終行のA,B,Cは一つ前の式のカッコ内にそれぞれ対応しています。A,B,Cはすべて係数ですから、解の公式でaが求まります:
貫通点は通常2点ありますので、aは2つ出てくるわけです。レイが円柱に接する時にaは重解になります。ここから貫通点Q1、Q2はそれぞれ、
と算出されます(一時的にLを原点にオフセットしていたので、それを戻しています)。レイが進む方向はa>=0.0なので、上式のQ1の方が先、つまり貫通開始点です。一方のQ2は貫通終了点となります。
③ 関数公開
レイと無限円柱との貫通点を算出する関数を公開します:
レイと無限円柱の貫通点を算出 // lx, ly, lz : レイの始点
// vx, vy, vz : レイの方向ベクトル
// p1x, p1y, p1z: 円柱軸の1点
// p2x, p2y, p2z: 円柱軸のもう1点
// r : 円柱の半径
// q1x, q1y, q1z: 貫通開始点(戻り値)
// q2x, q2y, q2z: 貫通終了点(戻り値)
bool calcRayInfCilinder(
float lx, float ly, float lz,
float vx, float vy, float vz,
float p1x, float p1y, float p1z,
float p2x, float p2y, float p2z,
float r,
float &q1x, float &q1y, float &q1z,
float &q2x, float &q2y, float &q2z
) {
float px = p1x - lx;
float py = p1y - ly;
float pz = p1z - lz;
p2x = p2x - lx;
p2y = p2y - ly;
p2z = p2z - lz;
float sx = p2x - px;
float sy = p2y - py;
float sz = p2z - pz;
// 各種内積値
float Dvv = vx * vx + vy * vy + vz * vz;
float Dsv = sx * vx + sy * vy + sz * vz;
float Dpv = px * vx + py * vy + pz * vz;
float Dss = sx * sx + sy * sy + sz * sz;
float Dps = px * sx + py * sy + pz * sz;
float Dpp = px * px + py * py + pz * pz;
float rr = r * r;
if ( Dss == 0.0f )
return false; // 円柱が定義されない
float A = Dvv - Dsv * Dsv / Dss;
float B = Dpv - Dps * Dsv / Dss;
float C = Dpp - Dps * Dps / Dss - rr;
if ( A == 0.0f )
return false;
float s = B * B - A * C;
if ( s < 0.0f )
return false; // レイが円柱と衝突していない
s = sqrtf( s );
float a1 = ( B - s ) / A;
float a2 = ( B + s ) / A;
q1x = lx + a1 * vx;
q1y = ly + a1 * vy;
q1z = lz + a1 * vz;
q2x = lx + a2 * vx;
q2y = ly + a2 * vy;
q2z = lz + a2 * vz;
return true;
}
上プログラムでは逐一内積計算等をしていますが、ベクトル型の変数(D3DXVECTOR3など)で置き換えるともっとスッキリします。
さて、前章でレイと球を、そして本章でレイと円柱との貫通点を算出できるようになりました。これで「レイとカプセルの衝突点」を計算できるはずです。