基礎の基礎編
その3 平面の捉え方
平面は色々な表現の仕方があります。それは平面が何によって決定されるかによって違ってきます。ここでは、平面をどう捉えたらよいかを考えて見ましょう。
① 平面の方程式
高校の数学の授業のようで恐縮ですが、平面の方程式についてまとめます。どうしてここで平面の方程式を持ち出すかと言うと、実はDirectXのヘルパー関数は平面の方程式を基本に考えているからなのです。3Dゲームを作成するにはどうしても触れなくてはならない部分なのでご了承下さい。
一般に平面は次の式で表されます。
a(x-x0) + b(y-y0) + c(z-z0) = 0
この式、正直ぱっとしないのですが、実はn=(a, b, c)が平面の法線ベクトルに相当します。そして、P0(x0, y0, z0)が平面上の一点なんです。そう考えるとこの式もちょっと分かりやすい気がしてきます。
さて、この式をちょっと展開します。
ax + by + cz = a*x0 + b*y0 + c*z0
右辺をdと置くと、
ax + by + cz = d
これが平面の一般式と呼ばれるものです(ax + by + cz + d = 0とも書きます)。ところで、右辺のd・・・いったい何なのでしょうか?
d = a*x0 + b*y0 + c*z0
これは法線ベクトルnとv=(x0, y0, z0)の「内積」です。内積は、
n・v = |n||v|cos(θ)
でしたね。これより、内積の答えであるdの値を|n|で割った値は、原点から平面までの距離であることがわかります。これ、次のお話しに関わる重要な点です。
左辺側のax + by + cz も内積の式になっています。(x,y,z)には空間の任意のP1(x1, y1, z1)が入ります。ここで、下の図をご覧下さい。

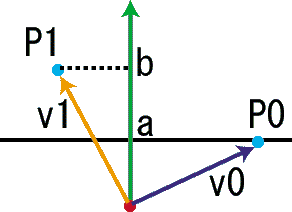
図中の赤い点は原点で、黒い横線は平面を水平に見た状態を表しています。緑色の矢印は平面の法線ベクトルです。平面の方程式では平面上の点P0が定められていました。右側の点ですね。原点からこの点までをベクトルv0と定めます。dはv0と法線ベクトルnとの内積でした。一方空間の適当な点P1を左辺に入れた式は、v1(オレンジのベクトル)とnとの内積になっています。
v0とnの内積であるdを|n|で割った値は、上の図だとちょうど原点からaまでの距離にあたります。これと同じ考えでいくと、v1とnの内積を|n|で割った値は、原点からbまでの距離と言うことになります。
つまり、平面の方程式の左辺に適当な点P1を入れた結果がdよりも大きければ、その点は平面の表側、小さければ平面の裏側にいることが判定できるのです。もちろんdと等しくなれば、それは平面上にあると言えます。
ここで平面の方程式を、
ax + by + cz + d' = 0
と書き直すと、この判定はもっと簡単になります。左辺に適当な点の座標を入れたとき、答えがプラスならば面の表側、マイナスなら裏側、0なら平面上に点があります。この性質は極めて重要です!
② 平面を4次元ベクトルとして扱う
平面の方程式は4つの係数(a,b,c,d)で表現できました。これは4次元ベクトルとして扱うことができます。すなわち、
vp = (a, b, c, d)
と考えます。こうすると、①で説明したベクトルとの関係をそこそこ気楽に考えることができます。例えば、点が平面の表裏どちらにあるかを判定するときは、点への位置ベクトルをv1=(x1,y1,z1,1)とすると、4次元ベクトルの内積、
vp・v0 = a*x1 + b*y1 + c*z1 + d*1
から一撃で求められます(符号で判断)。点の位置ベクトルの4つ目を1にするのがポイントです。
他にはv1=(x1,y1,z1,0)とすると、
vp・v0 = a*x1 + b*y1 + c*z1 + d*0 = a*x1 + b*y1 + c*z1
となり、これは平面の法線ベクトルとベクトルv1の内積、つまりは角度の関係を見ることができます。v1が別の平面の法線ベクトルだとすれば、平面同士の角度の関係を表すことにもなります。
こんなことを書いているのも、実はDirect3DXのヘルパー関数にこれを行ってくれる関数があるためで、間違いを犯さないために確認をしてみました。