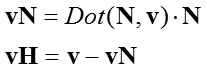
運動編
その2 壁に投げたボールの反射
球と球と同じくらい誰でもやりたいのが「壁と球の衝突」です。これがあると、ある入れ物の中に球を放り投げて遊ぶことができるようになります。
壁は言ってみれば平面状にずら~っとならんだ点の集まりです。そして、球であれば壁と接するのはただ1点です。つまり、瞬間的には壁と球の衝突と言うのは質点同士の衝突とみなすことができます。ただし1つ決定的に違う点があります。多くの人は、壁に球が当たったら「球は動くが壁は不動」でありたいと考えます。壁まで動き出したら世界がぐちゃぐちゃになってしまうからです。ビリヤードのクッションに球が当たった瞬間にクッションがどこかに飛んでいったら「勘弁してくれ~」となりますよね(笑)。そこがこの章のポイントにもなります。
では、早速行ってみましょう~。
① 壁の定義
ここで言う壁は無限、もしくは有限の範囲を持った平面を指します。無限の壁は空間を半分に分けますし、有限の平面はポリゴンを構成できます。無限と有限とで違うのは当たり判定の計算方法です。無限の壁はその法線だけで球との当たり判定ができます。一方ポリゴンは球がその有限の範囲に当たっているかをさらに検討する必要があります。
② 動かない壁の「反発係数」が鍵
地面に板を置きその上に球を落として衝突させた時、その衝突直前と直後の速度差の比を取ると反発係数を測定できます。今回板は不動で、衝突前後で速度は変化しないと考えたいので、板と球の反発係数は純粋に球の速度差の比となります。もし垂直に板に落とした球が同じ速度で反発すれば、反発係数は1になります。逆に垂直方向に球が跳ねなければ、反発係数は0です。
壁に球が斜めに入った時、反発係数は板に対して垂直方向の速度ベクトルの「減少度」をもたらします。板に対して水平方向の速度ベクトルは板との反射には関与しません(摩擦があれば別です)。これは壁と球との反射では主に垂直方向の動きに注目すれば良い事を示しています。
④ 壁が動くと球が動くのは同じ事
箱を揺らす(平行移動)などして壁が球に向かうように当たるというのは、見方を変えれば球が壁に向かってきたと考える事ができます。
複線で同じ方向に走っている電車はとまって見えます。一方反対に走ってきた電車の速度はとても速く感じます。これは、運動が持つ「相対性」を良く反映しています。相対性というのは、あるものを基準にして初めて別の物の速度が決まる事を行った原理です。
今、動いている壁を基準にして壁目線で球を見ると、止まっている球は壁に迫って来るように見えるはずです。これは、「球が動いている」と考えても何も差し支えありません。どういう方向に動いているかと言うと壁の動きと真反対の方向です。壁の速度ベクトルをv_wall、球の速度ベクトルをvとするなら、壁から見た球の相対速度ベクトルはv-v_wallとなります(相対速度はいつも[相手]-[基準])。つまり両方が動いている状態は面倒なので、つねに壁を基準にして球のみが動いて衝突していると考えると多方面でいろいろと楽になります。ただし、これによって求めた垂直成分の速度ベクトルは球の相対速度ですから、これをワールドの目線に戻すためには相対速度を元に戻す、つまり相対速度に壁の速度を足さないといけません。細かいことは次からの例題でお話します。
⑤ 例題:固定壁に質点を当てる
最初の例題は、ワールド空間にある固定した壁に質点をまっすぐに飛ばして当てる処理です。基本中の基本ですね。壁が止まっている時の一般式を出したいので、あえて変数で話を進めていきます。
法線Nを持つ壁と質点が衝突したとします。この時の質点の入射ベクトルをvとします。反射は垂直方向のみが影響されるので、まず入射ベクトルを壁に垂直なベクトルvNと水平なベクトルvHに分解します。vNは壁の標準化法線Nと入射ベクトルとの内積Dを取り、それを標準化法線に掛け算すると得られます。標準化したベクトルと内積をとると、そのベクトルに射影した長さを得る事ができます。今Dは常にマイナスになりますので(法線と入射角は常に鈍角であるため)、標準化法線にDを掛けると法線は逆さまを向きます。それがちょうどvNに該当する事になるわけです。
一方水平なベクトルvHは、vH+vN=vであるので、vH=v-vNとして求めます。以上をまず式としてまとめるとこうなります:
これで、衝突直前の速度を垂直と水平に分離できました。
衝突後、vNは真逆になり(符号反転)、その大きさは反発係数eの分だけ減少してしまいます。つまり、衝突後の垂直ベクトルvN'はvNに-eを掛けると算出できます。後はこれとvHを足し算すれば、欲しい衝突後の速度ベクトルv'が出てきます。式はこちら:
このv'の右辺をどんどん展開していくと、最終的に次の一般式が得られます:
これが衝突後の反射ベクトルを一発で求める式です。内積1回だけですからえらい簡単ですね。
⑥ 例題2:迫り来る壁
今度は動く壁と質点の反射です。先ほどの壁が速度vWで平行に動いているとしましょう。また質点の速度をvPとしておきます。ここから衝突の瞬間の質点の相対速度vは、v=vP-vWと表せます。
相対速度vにすると、壁は止まっている状態と考えられますので、⑤で導いた式がそのまま使用できます。求めた反射速度ベクトルv'は、止まっている壁から見た速度です。実際には壁も動いていますので、それを元に戻す必要があります。これはv'にvWを足し算するだけです。
以上から双方が動いているとした時の反射後の速度ベクトルを求める一般式は次のようになります:
最下段の導出式を見ると、なるほど内積部分で衝突の力の計算が終わっていますね。結果はとてもシンプルになりました。
本当は回転する壁などもやりたいのですが、これは質点ではなくて「剛体」の話になってしまいますので、ここではやめておきます。
⑦ 平面と球の衝突後速度算出関数
最後に平面と球の衝突後の速度算出関数を公開致します。この関数はコピペするとすぐに使えます。ちなみに壁が動かないバージョンです。
平面と球の衝突後速度算出関数 ///////////////////////////////////////////////////
// 平面と球の衝突後速度算出関数
// pColliPos : 衝突中のパーティクルの中心位置
// pVelo : 衝突の瞬間のパーティクルの速度
// weight : パーティクルの質量
// res : パーティクルの壁に対する反発率
// time : 反射後の移動可能時間
// pNormal : 平面の法線
// pOut_pos : パーティクルの反射後位置
// pOut_velo : パーティクルの反射後速度ベクトル
bool CalcParticlePlaneAfterPos(
D3DXVECTOR3 *pColliPos,
D3DXVECTOR3 *pVelo,
FLOAT res,
FLOAT time,
D3DXVECTOR3 *pNormal,
D3DXVECTOR3 *pOut_pos,
D3DXVECTOR3 *pOut_velo
)
{
// 反射後速度を算出
D3DXVECTOR3 N;
D3DXVec3Normalize(&N,pNormal);
*pOut_velo = *pVelo - (1+res)*D3DXVec3Dot(&N,pVelo)*N;
// 移動位置を計算
*pOut_pos = *pColliPos + *pOut_velo * time;
return true;
}
壁と球との衝突箇所さえわかれば、後は質点と同じ式で反射ベクトルが求まります。これに重力なども加味すれば、坂道をバウンドしながら転がる(ように見える)球なんかも表現できます。さらに球と球の衝突も入れれば、もう坂道を沢山転げ落ちてお互いバンバンぶつかり合う表現も可能です。そうなると、いや~これは楽しいですね~。