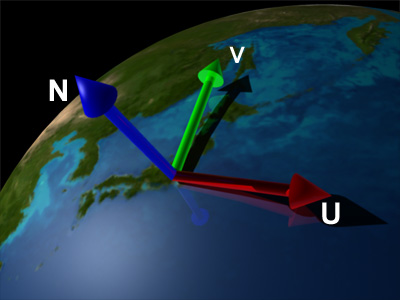
東京に乗っけてみました(^-^;
ホーム < ゲームつくろー! < プログラマブルシェーダ編
その12 頂点座標とUV座標から接ベクトルを求めるちょっと眠い話
3Dモデルのポリゴン表面を凸凹に見えるように貼るバンプマップ。この貼り付け時に絶対に必要なのが接ベクトル(Tangent Vector)です。
接ベクトルというのは「接ベクトル空間(Tangent Vector Space)」という座標空間で表されたベクトルの事です。接ベクトル空間と言うと難しそうですが、下図のように単に3Dモデル表面のある1点に乗っかっている座標空間です:
東京に乗っけてみました(^-^;
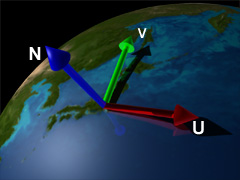
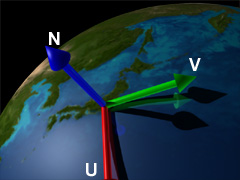
上の図では地球表面上の東京の上に接ベクトル空間を設けてみました。ただ、表面上の一点に設けると言っても色々な設け方があるはずです:
 |
 |
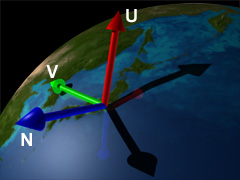 |
上のどれも接ベクトル空間として成り立ちます。しかしこれが法線マップやバンプマップなどポリゴン表面にテクスチャを貼り付ける時にはその軸の向きが非常に大切になります。なぜなら、法線マップは接ベクトル空間の軸を規準にその方向を決めているからです。例えば左の図の緑色の軸方向に法線が傾いているのが正しい時に、接ベクトル空間を真ん中や右図だとしてしまうと、緑色の軸が全く別方向を向いているため、ライティング計算が狂ってしまいます。ですから、接空間の軸を適当に決めてはいけないんです。接空間の特にUとVの軸は「ローカル座標にあるモデルに貼り付けたテクスチャの向きと一致させる」事が必要不可欠なんです。
ポリゴンの頂点を指し示した時、そこに貼られているテクスチャの(局所的な)向きを判断し、その接ベクトル空間の各軸の方向を決めるにはどうしたら良いのか?この章の目的はそこにあります。これを知るにはどうしてもちょっとだけ数学のお話が必要になります。なるべく簡単に(厳密性を欠きますが)噛み砕きたいのですが、どうしても眠くなる章です。ゆっくり上からご覧下さい(^-^)。
① 1つの頂点に5つの座標情報
3Dモデルがあるのはローカル空間、テクスチャがあるのはUV空間です。UV座標は1つの頂点に対応して定められるので、1頂点にはローカル座標値x,y,zとUV座標値u,vの5つの座標情報が埋め込まれていることになります。逆に言うならば、実は座標に関する情報はそれしかありません。ポリゴンのある1頂点を記号で表すと、例えば次のようになります:
今私たちがやりたいのは『1つのポリゴンの頂点座標とUV座標の情報から、接ベクトル空間の各軸の方向を一意に定める』事です。それを実現する方法を知るために、まずは下の2図をご覧下さい:
これは1つのポリゴンに定義された頂点情報と各軸を描いたものです。左の図と右の図とで、ポリゴンのローカル座標(x,y,z)は全く一緒ですが、テクスチャの貼り方(貼る方向)が異なっています。左の図は貼る方向がローカル軸と平行ですが、右図は45度傾いています。
まず左の図のP0に注目です。ここからU軸方向に進むとP2に到着し、U軸方向に0.8進んだのがわかります(赤い数字の差分です)。この時のローカル座標の増分はそれぞれ(Δx, Δy, Δz ) = ( 14, 0, 0 )となります。面白い事にこのローカル座標の増分をベクトルとみなすと、それはU軸の方向を向いています。後の便宜上上の増分をU軸の増分で割っておきます:
右の図でも同じ事をしてみましょう。今度はP2に注目です。ここからV軸方向に進むとP0に達します。ローカル座標だと斜めに進んでいる状態です。この時Vの増分は0.5。対してローカル座標の増分は( -8, 8, 0 )。どうでしょう、これもやっぱりV軸のベクトルになっていますよね。このように、ある頂点に注目して、そこから「UもしくはV軸方向」に進んだ時のローカル座標の増分(差分)は、その軸のその頂点でのローカル座標での向きになります。
『ある軸方向にちょこっと進んだ時の他の変数の増分』というのは、まさに微分の考え方です。上の例では頂点の差を取りましたが、これは別に本の少しの差分でも十分です。それが極限まで小さくなっても状況は変わりませんので、先ほどの差分は必然的にこう書き直せます:
偏微分の記号(∂:ラウンド)はある軸方向の増分だけに注目した場合の微分です。上ではU軸方向に動かした時の増分に注目しているのでこうなります。
さてここまでの導きから、何らかの式を立てて上のような微分ができると、UやV軸のローカル座標での方向がビシッと定まりそうです。後はローカル座標の(x,y,z)をuやvで表す式を考えることになります。
② ローカル座標をUV座標で表す
ローカル座標にあるポリゴンは言わずもがなの平面です。三角ポリゴンを形成する3つの頂点も、もちろん1つの平面の上に乗っかっています。今、頂点は5つの座標値で表現されていました:
ここでうまい事を考えます。5つの成分のうち、例えば(x, u, v)の3成分だけに注目し、3頂点から平面を作ってみます。平面は点の数が3つあればできるわけです。平面の方程式にすると、
です。両辺をD0で割ると正規化されて、
となります(ABCの記号が同じ添え字なのは目を瞑ってください(^-^;)。このABCは未知の係数ですが、今頂点が3つあるので解く事ができます。連立方程式を立てても良いのですが、平面の方程式の(A,B,C)は平面の法線である事を利用すると、ポリゴンの法線から一発で求まります。
なんでこんな事をしているのか?それは、上の平面の式を変形すると見えてきます。上式を左辺にx、右辺にそれ以外を持ってくると、面白い事にローカル座標がUV座標で表せてしまいます:
ここまで来るとやりたい事が大体見えますね。①の最後に示した偏微分が可能になるわけです。すなわち、
となるわけです。嬉しいことにこれは「定数」です。これと同様の事をyやzについても行うと、U軸及びV軸のローカル座標での方向は次のように平面の方程式の係数だけで表せてしまいます:
A1、B1、C1はyについて、A2、B2、C2はzについての係数です。あれよあれよという間に、気が付けば接ベクトル空間のU軸とV軸の方向が定まってしまいました(^-^)/。眠い話はここまでで終わりです。
③ 3頂点のローカル座標とUV座標からU軸(Tangent)とV軸(Binormal)を求める関数を公開します!
これで、ローカル空間にあるポリゴンに貼られたテクスチャの方向性にちゃんと沿った接ベクトル空間の軸が定まりました(N軸は法線でOK)。せっかくなので、これらの軸を求める関数を公開します。ご自由にお使い下さい:
| U軸とV軸を求める関数 |
| // 3頂点とUV値から指定座標でのU軸(Tangent)及びV軸(Binormal)を算出 // // p0, p1, p2 : ローカル空間での頂点座標(ポリゴン描画順にすること) // uv0, uv1, uv2 : 各頂点のUV座標 // outTangent : U軸(Tangent)出力 // outBinormal : V軸(Binormal)出力 void CalcTangentAndBinormal( D3DXVECTOR3* p0, D3DXVECTOR2* uv0, D3DXVECTOR3* p1, D3DXVECTOR2* uv1, D3DXVECTOR3* p2, D3DXVECTOR2* uv2, D3DXVECTOR3* outTangent, D3DXVECTOR3* outBinormal ) { // 5次元→3次元頂点に D3DXVECTOR3 CP0[ 3 ] = { D3DXVECTOR3( p0->x, uv0->x, uv0->y ), D3DXVECTOR3( p0->y, uv0->x, uv0->y ), D3DXVECTOR3( p0->z, uv0->x, uv0->y ), }; D3DXVECTOR3 CP1[ 3 ] = { D3DXVECTOR3( p1->x, uv1->x, uv1->y ), D3DXVECTOR3( p1->y, uv1->x, uv1->y ), D3DXVECTOR3( p1->z, uv1->x, uv1->y ), }; D3DXVECTOR3 CP2[ 3 ] = { D3DXVECTOR3( p2->x, uv2->x, uv2->y ), D3DXVECTOR3( p2->y, uv2->x, uv2->y ), D3DXVECTOR3( p2->z, uv2->x, uv2->y ), }; // 平面パラメータからUV軸座標算出 float U[ 3 ], V[ 3 ]; for ( int i = 0; i < 3; ++i ) { D3DXVECTOR3 V1 = CP1[ i ] - CP0[ i ]; D3DXVECTOR3 V2 = CP2[ i ] - CP1[ i ]; D3DXVECTOR3 ABC; D3DXVec3Cross( &ABC, &V1, &V2 ); if ( ABC.x == 0.0f ) { // やばいす! // ポリゴンかUV上のポリゴンが縮退してます! _ASSERT( 0 ); memset( outTangent, 0, sizeof( D3DXVECTOR3 ) ); memset( outBinormal, 0, sizeof( D3DXVECTOR3 ) ); return; } U[ i ] = - ABC.y / ABC.x; V[ i ] = - ABC.z / ABC.x; } memcpy( outTangent, U, sizeof( float ) * 3 ); memcpy( outBinormal, V, sizeof( float ) * 3 ); // 正規化します D3DXVec3Normalize( outTangent, outTangent ); D3DXVec3Normalize( outBinormal, outBinormal ); } |
気をつけたいのが、引数の頂点座標もしくはUV座標が完全に重なっていると関数が失敗する点です。座標が重なるという事は、三角ポリゴンが縮退してしまっているじょうたいです。こうなると面の法線が不定になるため、計算が成立しません。上の関数のASSERTで止まった場合は3Dモデルをしっかりチェックすべきです。
接ベクトル空間は本当はもっと厳密な数学の上で展開されますが、3Dゲームの接ベクトルを求めるのであれば上の知識で十分です。公開関数もありますので、必要になった時にそれを使用すれば良いかなと思います。ただ、こういうものの背景をある程度捉えておく事は3Dゲームを作る上で大切な心がけだと思いますので、ブラックボックスにせずに一度体験して習得しておきたいですね。