ホーム < ゲームつくろー! < プログラマブルシェーダ編
シェーダ編
その3 深度バッファの精度を上げる
深度バッファ(デプスバッファ)はカメラで撮影したモデルまでのZ距離を表したテクスチャです。シェーダを使っているといろいろな場面に出てきます。通常Z距離はカメラが捉えられる最遠距離Z_farと最近距離Z_nearを用いて0〜1の間に標準化されます。
深度バッファは影の生成やDoF(被写界深度)などで必須ですが、この時問題になるのが深度バッファの精度です。通常深度値はRGBAのどれか1色にその値を穿つので、テクスチャフォーマットによってその精度が大きく変わってしまいます。現行(2007/11)で最も良い精度を出してくれる一般的なテクスチャフォーマットは64bit浮動小数点テクスチャです。これは16bitの浮動小数点を4つ使用してピクセルの色の幅(ダイナミックレンジ)を大幅に向上させることができるテクスチャです。これで表現された深度はかなり精度が高いといえます。しかし、このフォーマット形式がサポートされているビデオカードは現行でそれ程多くはありません。32bit浮動小数点テクスチャならばまだサポート率が高いかもしれません。しかしこれは一色を8bitの浮動小数点とするフォーマットなのでかなり精度が落ちます。
これら浮動小数点テクスチャが扱えない環境の場合、いわゆるR8G8B8A8フォーマットで深度を表現する事になります。しかし、このフォーマットは1色を8bitの整数で表現するだけなので、0〜1の小数点を256段階の精度に落としてしまいます。こうなると、綺麗な影やDoFはまず期待できなくなってしまいます。これは何とか精度向上をはかりたいわけです。
この章では整数テクスチャフォーマットで深度バッファの精度を上げるにはどうしたら良いのか考えてみます。答えは割と簡単なんですけどね(^-^;
① 各色のビットを有効に使う
題目が答えです。思った通りの答えで興ざめですいません(^-^;。32bit整数テクスチャはせっかく32bitもあるのですから、それを有効に使って深度の分割数を細かくしてしまえばいいんです。
まず深度書き込みのおさらいです。深度は「射影変換した頂点座標のZ値をW値で割る」というお決まりの計算で算出します。頂点座標の変換は頂点シェーダで行いますが、この計算は頂点シェーダではなくてピクセルシェーダで行います。そのために頂点シェーダでテクスチャ座標(TEXCOORD)にZ値とW値を刻印します:
深度計算頂点シェーダ struct OUTPUT_VS {
float4 pos : POSITION;
float4 texCoord : TEXCOORD0;
};
float4x4 WVP : WorldViewProjection;
OUTPUT_VS ZCalc_VS( float4 inPos : POSITION )
{
OUTPUT_VS out = (OUTOUT_VS)0;
// 頂点変換
out.pos = mul( inPos, WVP );
// 深度に必要な値をテクスチャ座標に記録
out.texCoord = out.pos;
return out;
}
頂点シェーダでout.texCoordに登録した頂点位置は、ピクセルシェーダで線形補間されて渡されることになります。これによりピクセルシェーダで正確なZ値を得る事ができますので、それをW値で割って0〜1まで標準化された深度を算出します:
深度計算ピクセルシェーダ float4 ZCalc_VS( float4 texCoord : TEXCOORD0 ) : COLOR0
{
// 深度算出
float depth = texCoord.z / texCoord.w;
return float4(depth, 0.0f, 0.0f, 0.0f);
}
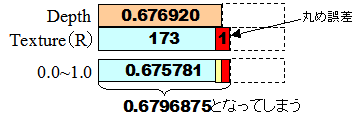
さて、上でdepthとして求めた深度値は0〜1の浮動小数点値です。その算出深度をR成分に穿って出力していますが、レンダリングターゲットが32ビット浮動小数点ならば十分な精度で出力されますが、これがR8G8B8A8の整数テクスチャならば一色8bitであるために「1.0/256=0.0390625」の単位に丸められてしまいます:
上の図でDepthがZ/Wで算出した真の深度です。これを8bitのR成分に代入すると水色の部分+赤い部分に丸められてしまいます。このテクスチャを再度利用する時には、もはや真の数値ではなく一番下にある0.679678...となってしまいます。本来は水色の部分と黄色い部分が正しいはずです。そこで上の図でちょぴっと出ている黄色い部分の情報をG成分に置く事を考えてみます。
黄色い部分は「真のDepth-水色部分」です。青い部分はDepthの値を1/256単位で丸めて算出します。これにはround関数を使います:
Depthの丸め値を知る float R = round( Depth * 256.0f );
R /= 256.0f;
Depth*256で173.***と0〜256範囲となりますが、round関数で173.0に丸められます。この値を256.0fで割ると下の173に対応する小数点値(0.675781)が出てきます。ここから黄色い部分は、
Depthの残差部分を求める float Def = Depth - R;
と算出されます。
さて、この黄色い部分の最大値は1/256です。よって、そのままG成分に入れると小さ過ぎて0になってしまいます。そこでこれを256倍します。すると0〜1の範囲になりG成分にちゃんと値が入ります。黄色い部分について256倍した状態を下図に示します:
先のDepthの値の場合、黄色い部分はおよそ0.291のようです。これをそのままテクスチャのG成分に保存すれば「75」として丸められます。ただ、やはり上図の緑色の部分に残差が含まれます。これはR成分と同じようにround関数で丸めて「74」に当たる0.289...を抽出し、残差をB成分に入れるように計算します:
G成分と残差を求める float G = round( Def_R * 256.0f * 256.0f ); // 74が出てくる
RoundValue_G /= 256.0f; // 0.289が出てくる
float Def_B = Def_R * 256.0f - RpundValue_G; // Def_R * 256が0.291..です
同様にするとTexutre(A)にも残差の丸め分を刻印できます。32bitだとここまでで計算は終り。都合4回の計算で、深度の精度は理論上では256段階から42億段階に格上げされた事になります。もちろんfloat計算なので浮動小数点誤差は出ますが、256段階よりははるかにはるかにマシです。
この4段階の計算をさせた深度シェーダはサンプルプログラムに挙げましたので参考にしてみて下さい。
② 32bit深度から深度を戻す
①の計算で深度はRGBA=(173, 74, 161, 14)と整数値となってテクスチャに登録されます。この深度テクスチャを他のシェーダで利用する時にはRGBA=(173/256, 74/256, 161/256, 14/256)と標準化されてサンプリングされます。この値から元の0.676920という深度(の近似値)に戻してみます。
まずR成分はそのまま使えます。これは一番粗い丸め値ですよね。次のG成分はR成分の残差を256倍してテクスチャに穿たれていますので、逆に256で割ると元の残差になります。同様にB成分は65536、A成分は65536*256で数値を割ると、それぞれの残差に戻ります。後はそれらを全部足せば良いだけです。この計算をExcel上で行ってみると、戻した値は0.67692と上手い事元の値にぴったり戻りました。実際はfloat型の誤差が出ますが、実用上は問題ないレベルになるはずです。
元に戻す部分を関数化すると次のようになります:
32bit深度値を求める float Convert_Color_To_Z( float4 color )
{
return color.r + (color.g + (color.b + color.a/256.0f) /256.0f) / 256.0f;
}
深度の精度を32bitまで高めるかどうかは作成するゲームの質やパフォーマンスで判断すれば良いと思います。16bit精度でもかなり綺麗になります。一時レジスタ数の上限がもしかするとからむかもしれませんが、これはシェーダバージョンが3.0以上だとまず問題にはならないでしょう。
③ 深度の精度はNear-Far比で驚くほど落ちる
精度の上昇がどれほどのものなのかを実感する解析結果を挙げます。興味のある方はどうぞ。深度の値とZ値は比例しません。一般にはカメラに近い部分ほど前後が正確である必要があるため反比例の関係になっています。
深度の算出式は、
で表されます。Vzはカメラから見たモデルまでのZ値、ZnとZfはそれぞれカメラが切り取る空間のNear-ZとFar-Zです。この式を使って深度の精度を体感してみましょう。上の式からVzを抽出すると次のようになります:
これは深度DepthからVzを求める式です。テクスチャ精度が256段階だったとすると、Depthの単位は1/256となります。そこでDepthが0.5、つまり深度の丁度真ん中までの時のZ値がどのくらいの距離になるかを計算してみましょう。Zf=10000m=10kmと固定しておいて、Znを0.1m、1m、10m、100m、1000mとしてみます。それぞれの計算結果は以下の通りです:
Zf Zn Depth=0.5 Ratio 10000m 0.1m 0.200m 0.001% 10000m 1m 2.000m 0.01% 10000m 10m 20.000m 0.1% 10000m 100m 198.020m 1.0% 10000m 1000m 1818.182m 10.10%
かなりびっくりする結果になりました。Depth=0.5の地点までの距離が驚くほど短いのが分かりますでしょうか。例えばZn=0.1m=10cmとした時、深度の真ん中はなんと20cm。つまりZnから10cmの間だけで深度の半分を使ってしまっているんです。残りの9999.9mくらいを128分割で表している事にもなります。反比例の怖さがここに見えますね。
Zfを1000m=1kmにするとどうなるか?これは意外な結果になります:
Zf Zn Depth=0.5 Ratio 1000m 0.1m 0.20m 0.01% 1000m 1m 2.00m 0.10% 1000m 10m 19.80m 1.00% 1000m 100m 181.82m 9.10% 1000m 1000m *** ***
最遠のZfとの割合(Ratio)で見ると10倍の改善は見られますが、10kmの時とDepth=0.5の絶対距離が殆ど変化していません。つまり、Zfを短くすると遠い距離での深度の解像度のみが改善される事になります。近場の解像度が足りない時、変えるべきはZfでは無くてZnというわけです。
では、次にテクスチャの解像度の違いによる改善を見てみます。Zf=10000m、Zn=1mとして、最も遠い位置の一歩手前の1解像度、そしてその前の1解像度がどれだけの長さになるのかを解像度の違いで算出してみます:
bit Last span Pre-last span 8 9750.37m 123.24m 16 1323.76m 1014.26m 24 5.96m 5.95m 32 0.0234m 0.0234m
これは興味深い結果です。256段階(8bit)だとなんと最後の1解像度は9750mです。そしてその1歩前が123m。Zn=1mの深度は恐ろしくゆがんでいる事がここからわかります。それでも8bitだと120mくらいを同じ深度とみなすわけですから、遠い方の深度比較は全く当てにならないわけです。16bitでも最後は1000m単位になるようです。16bitでも遠方は厳しいですね。でも、それ以上のbitになると深度の精度は劇的に改善されます。32bit精度にすると最遠でも2.4cmを区別できます。10kmの2.4cmですから十分過ぎる精度と言えるでしょう。もちろん近場の精度は驚異的なはずです。さすが42億段階(^-^)。
上の計算結果は浮動小数点誤差を考えていませんが、解析結果からも256段階の深度にする理由はもう無さそうです。32bitは多少計算負荷がありますので、これを24bitに落としても実用上は十分なはずです。皆さんも色々と調節をして適切な深度バッファ精度を試してみてください。この章のサンプルプログラムもつけましたのでご参考にどうぞ。
(2007. 12. 21追記)
④ 色々後書き
さて、記事を書いてしばらくして、お仕事の中で実際に深度の精度を上げる必要が出てきました。そこで色々調べますと、先の実装は組み込み関数を使うことでもっと楽になる事が分かりました。また先の方法はRGBAの「A」に格納する値まで計算していましたが、実際はそこまでする必要が無いようです。それは、float型の仮数部が23bitの精度しかないため、24bit目まで計算すれば十分なためです。つまりRGBまで計算するだけで事足ります。
より簡単な実装に使う組み込み関数はmodf関数です。これは次のように定義されています:
modf関数 modf( x, out ip )
xは何らかの小数点値です。これはfloat4型などベクトル型でも構いません。
ipには「out」という接頭子が付いていますが、これはここに値が戻ってくるという意味を指しています。ipにはxの小数点部が戻ってきます。
modf関数の戻り値はxの整数部です。つまりこの関数は浮動小数点を整数部と小数部に分離してくれます。例えば、
float int_res;
float float_res = modf( 126.5521, int_res )
とすると、int_resには126が、float_resには0.5521が格納されます。
これを深度計算に利用すると次のようになります:
modf関数を使った深度計算 float4 unpacked_depth = float4(0, 0, 256.0f, 256.0f);
unpacked_depth.g = modf( depth*256.0f, unpacked_depth.r);
unpacked_depth.b *= modf( unpacked_depth.g*256.0f, unpacked_depth.g );
return unpacked_depth / 256.0f; // 標準化
まずunpacked_depthを初期化します。BA成分に256.0fを入れておく事がコツです。次の行でmodf関数を使いdepth*256を整数部と小数部に分けます。整数部はunpacked_depth.rに格納され、小数部はunpacked_depth.gに代入されます。これでr成分の値(0〜255の値)が決まります。unpacked_depth.gには差分が入っていますので、これをまた256倍して整数部と小数部に分離します。この時点でG成分(0〜255)も決まりです。またB成分には元々256.0fが入っていますので*=演算子でBの値も計算してしまいます。ここまでの計算でRGBAにそれぞれ0〜255の値が格納されています。それを最後に256.0fで割ることで0〜1に標準化される事になります。
上の計算は組み込み関数を使っているため一般に先のベタにやる方法よりも高速だと思われます。A成分を計算していませんが、それは冒頭に述べたようにfloat型の仮数部が23bitであるため、24bit以降の精度を求める意味がないためです。これによりさらに高速化されます。3行目で256倍して、returnで256で割っているのは意味が無いのではと思ってしまうかもしれませんが、こうしないと「/256」の回数が増えてしまいます。並列演算に特化しているGPUにとってfloat型の割り算4回とfloat4型の割り算1回は後者の方が圧倒的に速いんです。
ということで、ちょっと最適化してみました。サンプルプログラムには反映されていませんが、こちらの使用をお勧めします〜。