VisualStudio + Pythonでディープラーニング
画像のエラー判定できるかな?
(2019. 12. 30)
今回は「分類」についてです。ニューラルネットワークは出力層で沢山の値を出力します。この値は通常実数の何かになりますが、時にそれでは困る事があります。例えば、画像に映っている物を識別する場合、その出力は「犬」とか「猫」のようなカテゴリーになります。なので出力値が3.74とか言われても困ってしまう訳です。そこでそういう「カテゴリー分類」をする場合はそれ用の層の作り方をします。
ここでは疑似的な画像データを作り、そこにエラーを含めて出力層でそれを識別する装置を作りながらカテゴリー分類のニューラルネットワークの作り方を見ていく事にしましょう。
① 疑似画像データ
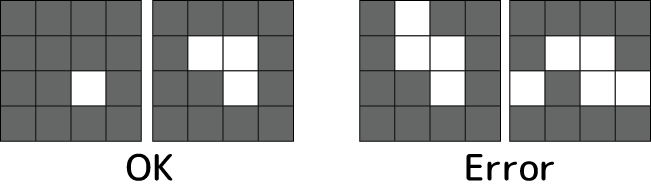
まずは入力となる疑似画像データを用意します。今回は次のような4×4の小さい画像をターゲットとします:
左側の方はOK画像で、右側の方はエラー画像です。OK画像は縁辺のマスが全部塗られています。一方エラー画像は縁辺のどれかに塗り残しがあります。そういうルールだとします。工業製品のエラー画像の簡易版と言った感じでしょうか。果たしてディープラーニングは縁辺の違いを認識しOKとErrorを正しく分類してくれるでしょうか?ちょっと楽しみです(^-^)
画像データと言ってもデジタルなので中身は単純な数値の塊です。上の画像も次のような1次元の配列として入力に与えます:
学習データはこの配列を動的にどばーっと作ります。作ったデータで縁辺となる0,1,2,3,4,7,8,11,12,13,14,15番の中に一つでも塗り残し(0)があったらエラー画像になります。ただランダムに作ってしまうと正解画像よりエラー画像の方が無茶苦茶多くなってしまうので、まずは全部1で初期化し、正解かエラーかを乱数で決め、正解だったら5,6,9,10の幾つかを適当に塗り残し、エラーだったら正解部分の塗り残しにエラー部分の塗り残しを加えます。
② 出力層は「OK」と「エラー」の2カテゴリー&Softmaxで
続いてモデルの構想です。入力層は画像の個々のピクセル16個の値を入力します。ニューロンの数は現段階で何とも言えませんのでN個としておきます。中間層の数も手探りする必要がありますのでM層とします。今回の問題は線形問題な気もしますが、一般的に分類は非線形である事が多いので、それを模して各層の活性化関数はReLUにしておきましょう。
最後の出力層では2つの出力を行います。一つはその画像がOKだったら1を返す事を期待し、もう一つはその画像がエラーだったら1を返す事を期待します。「互いに排反なんだから出力は1つで良いのでは?」と思うかもしれませんが、例えばエラー画像をもっと細かくカテゴリー分けするなどの拡張を考えると、それぞれのカテゴリーに対応した出力を設けた方が柔軟です。
で、ここが大変に重要な所で、出力層の活性化関数はSoftmaxにします。Softmaxは出力層に入って来る数値を確率的な値に変換してくれます。イメージはこちらをご覧ください。出力される数値をそのまま見てしまうと、OKが14.34でErrorが5.86のように判断しにくい事になりますが、Softmaxで変換するとOKが96.7%、Errorが3.3%のように人が判断しやすい値になります。モデルの判定自信度のような感じですね。
ここまでのモデルイメージはこんな感じでしょうか:
③ 交差エントロピー誤差評価関数
これまで評価関数には平均二乗誤差を使ってきました。正解との差の2乗を使う方法です。しかしカテゴリーなデータではそもそも「差」という概念がありません。「犬-猫」とか「正解画像-エラー画像」って意味が分からないですよね。そこで比較するカテゴリーを数値化する必要があります。これは「one-hot」と呼ばれる形式にするのが一般的です。別に難しい事はなくて、すでに上で考えたように正解とエラーの2カテゴリーを{正解,エラー} = {1, 0}, {0, 1}のようなゼロ・イチで表現します。こうすると{ 0.87, 0.13 }のような割と正解かも、みたいな中間的な推定値を取り扱う事ができるようになります。
正解が{ 1, 0 }に対して推定が{ 0.87, 0.13 }として、これがどれだけ正解に近いかどうやって計れば良いのでしょうか?それを可能にするのが「交差エントロピー誤差」で、次のような式で表現されます:
y'が正解の値、そしてyが推定値です。ただし正解も推定値も「確率」である必要があります。またyもy'もベクトルなので、これは内積です。先程の確率値で具体的に計算してみましょう:
こういう計算になります。これは統計学で言う「情報量」という指標値で、値が小さい程その結果が尤もらしいと判断出来ます。カテゴリー分類をする時には評価関数に交差エントロピーを使うのが一般的です。
では以上のニューラルネットワークモデルをKerasで組みます。
④ Kerasで実験
ここまでのお話をPythonで組んでみましょう:
import keras
import numpy
import random
# 画像作成
def createImage( image, okImage = True ):
#正解画像作成
okBit = random.randint( 0, 15 )
idx = [ 5, 6, 9, 10 ] #正解部分idx
for i in range( 4 ):
if ( ( okBit >> i ) & 0b1 == 1 ):
image[ idx[ i ] ] = 0
if ( okImage == False ):
#エラー画像化
eidxs = [ 0, 1, 2, 3, 4, 7, 8, 11, 12, 13, 14, 15 ]
n = random.randint( 1, 3 ) #塗り残し数
for i in range( n ):
e = random.randint( 0, 11 )
image[ eidxs[ e ] ] = 0
#モデル作成
model = keras.Sequential()
#入力層は16次元
layer1 = keras.layers.Dense( units = 10, activation="relu", input_shape=(16,) )
#中間層
layer2 = keras.layers.Dense( units = 10, activation="relu" )
#出力層
outputLayer = keras.layers.Dense( units = 2, activation="softmax" )
model.add( layer1 )
model.add( layer2 )
model.add( outputLayer )
#確率的勾配降下法で検索、交差エントロピー誤差で評価
sgd = keras.optimizers.SGD( learning_rate=0.05 )
model.compile( optimizer=sgd, loss="categorical_crossentropy" )
model.summary()
#学習データ作成
#4x4の疑似画像データをn枚作る
n = 1000
train_x = numpy.ones( (n, 16) )
train_y = numpy.zeros( (n, 2) )
for i in range( n ) :
if ( random.randint( 0, 1 ) == 0 ):
createImage( train_x[ i ], True )
train_y[ i ][ 0 ] = 1
else:
createImage( train_x[ i ], False )
train_y[ i ][ 1 ] = 1
print( train_x )
print( train_y )
#学習開始
model.fit( train_x, train_y, epochs=100 )
#実施テスト
m = 16
test_x = numpy.ones( (m, 16) )
answer = numpy.zeros( (m, 2) )
for i in range( m ) :
if ( random.randint( 0, 1 ) == 0 ):
createImage( test_x[ i ], True )
answer[ i ][ 0 ] = 1
else:
createImage( test_x[ i ], False )
answer[ i ][ 1 ] = 1
res = model.predict( test_x ) #テスト
print( test_x )
print( answer )
print( res )
モデル作成の所は特に問題無いかなと思います。先のモデル図に従って静々と作成しています。出力層のニューロン数を2に、活性化関数にSoftmaxを指定している所だけ注目です。モデルのコンパイル時に評価関数として交差エントロピー誤差("categorical_crossentropy")を指定しています。
あとは①で説明した疑似画像データを作成しています。具体的な作成プロセスはcreateImage関数に逃がしました。細々と乱数を使っていますが、やっている事はOK画像をまず作成し、エラー画像指定があれば縁辺セルの塗りをキャンセルしているだけです。そういう学習用の画像を1000枚用意し、それをモデルに食わせてフィッティングさせています。
さて、ではこのコードを実行した結果、テスト画像16枚をモデルはどう判定したか?出力を整理するとこうなりました:
すごい、判定率100%です!モデルは見事に縁辺部に塗り残しがあるか否かで画像を分類してくれました。中間層1枚ですが見事なもんです(線形性の強い問題というのもありますが)。
このようにニューラルネットワークで分類問題を解く時には、出力をカテゴリー数分の次元のOne-hotデータにして、出力層にSoftmx活性化関数を用いて交差エントロピー誤差で評価するのが基本セオリーです。入力が複雑になると単純な中間層だけだと対処できなくなるかもしれないので、層を増やすなど工夫は必要に思います。それにしても、ルールを教えている訳でもないのに傾向をちゃんと感じ取って分類してくれるというのは面白いもんですよねぇ~(^-^)