WebGL
板ポリ一枚をブラウザの世界に投下
HTML5の目玉機能の一つ「canvas」。画面に図形や絵など2Dを描くキャンバスを置けてしまう機能です。しかし、このcanvas君には「WebGL」という3Dを描画する機能も実はあります。WebGLは「GL」と名にあるようにOpenGLをベースとしたJavaScriptで書ける3D描画ライブラリです。WebGLをサポートしているブラウザであれば、原則的にはどのブラウザでも3D描画ができてしまうというのはゲーム屋として非常に興味深い所であるわけです。ただ、何をどうするか今の所さっぱりわかっていません。
そこで、まずはWebGLを通してブラウザの世界にポリゴン1枚を投下する所から始めようと思います。
① Canvasを置いてWebGLコンテキストを取る所からスタート
ゼロからスタートします。WebGLはHTML5のcanvasを用いて描画するのですから、何はともあれ「HTML5」なファイルが必要ですね。超最低限なHTML5は例えば以下のような記述になります:
最低限なHTML5 <html>
<head>
<meta charset="UTF-8">
</head>
</html>
ブラウザは<meta>に上にあるようにcharsetが指定されているだけだとHTML5としてくれます。このHTMLをChromeで起動しても、もちろん真っ白い画面が出るだけです。では、ここにcanvasを1枚置いてみましょう。置くcanvasは幅、高さ共に480とします:
canvasをブラウザに置く <html>
<head>
<meta charset="UTF-8">
</head>
<body>
<canvas id="canvas" width=480 height=480></canvas>
</body>
</html>
これだけです(^-^)。Chromeで見てもまだ真っ白のままですが、らしい位置を右クリックして「要素を検証」を選択すると、確かにそこにCanvasが置かれているのがわかります。さて、このcanvasの中には「コンテキスト」という描画関係のAPIを提供してくれるオブジェクトが潜んでいます。次はそれをJavaScriptで取り出します:
WebGL用のコンテキストを取得 <html>
<head>
<meta charset="UTF-8">
<script>
window.onload = function() {
// canvasからコンテキストを取得する
var canvas = document.getElementById("canvas");
var glc = canvas.getContext("webgl") || canvas.getContext("experimental-webgl");
}
</script>
</head>
<body>
<canvas id="canvas" width=480 height=480></canvas>
</body>
</html>
上の太文字部分に注目する前に、ここがwindow.onloadとして呼ばれる事に注目です。何故こうするのか?それはbody部分の解釈が終わった後にこのスクリプトを実行して欲しいからです。通常head部分はbody部分よりも先に解釈されます。そのため、onloadにしないとcanvasが世界に置かれる前にスクリプトが走ってしまいます。世界に"canvas"がまだ無いので、canvas変数はundefinedとなってしまい、結局エラーで終わってしまうんです。
上の太文字部分は、canvas要素を取りだし、それが持っている「getContext関数」を通してWebGL用のコンテキストを取得しようとしています。getContext関数の引数には取得したいコンテキストのタイプを文字列で指定します。上の例では"webgl"を指定しています。ただし、現行の(2012.11)ブラウザによっては"webgl"をサポートしていない物もあります。その場合には次の"experimental-webgl"を試してみます。これは名前にあるように実験的なWebGLライブラリです。
これでWebGL用のコンテキストを取得できたら、いよいよWebGLを開始出来ます!(^-^)/
② 毎フレーム回る仕組みを先に作ってしまいます
「さぁ3Dだぁ!」と勇みたい所ですが、ちょっと待った。上のままだとスクリプトが一回通るとプログラムが終わってしまいます。それでは何も面白く無いのです。動きのある物にするには描画部分を何度も回して更新してもらう必要があります。そこで、ゲームループとなる部分を先に作ってしまいます。尚、以後HTML部分の表記は冗長なので、スクリプト部分だけを抜き出します。
JavaScriptでのループはsetInterval関数で設定できます。毎回更新して欲しい関数をupdate関数として、それをsetInterval関数に登録します:
ゲームループを作成 window.onload = function() {
// canvasからコンテキストを取得する
var canvas = document.getElementById("canvas");
var glc = canvas.getContext("webgl") || canvas.getContext("experimental-webgl");
function update() {
// ゲームループ
}
setInterval( update, 33 );
}
これでupdate関数がおおよそ33msec.くらいの間隔で呼ばれ続けます。JavaScriptなので時間間隔は大変にいい加減です。ゲームもそれを見越す必要がありますが、今は気にせず次に進みますよ(^-^;
③ シェーダを書かないといかんのです!
WebGLには残念ながら固定機能(描画を楽にしてくれる人)はありません。描画を行うには頂点シェーダとフラグメントシェーダ(DirectXでいうピクセルシェーダ)という2つのシェーダを自前で書く必要があります。ん~と、ここで「え~」と思った方は、残念ながら脱落(^-^;。そういう時代です。
頂点シェーダというのは画面内に三角形なポリゴンを描画する「領域」を計算するプログラムです。三角ポリゴンが世界に置かれると、それはまずカメラに捉えられます。カメラはそれをスクリーンに投影する訳ですが、この時にカメラのアングルによって三角形ポリゴンは色々な見え方になります。その「画面内での見え方」を頂点シェーダで計算する事になります。
頂点シェーダで計算されたスクリーン内のポリゴン領域は「ラスタライズ」という処理が行われ(これはWebGL内で自動的に行われます)、最終的にその領域を占めるピクセル配列が作られ、順次フラグメントシェーダに渡されてきます。フラグメントシェーダではそのピクセルを「何色で描画するか」決めます。フラグメントシェーダが最終的に決めた色が、スクリーンに反映される訳です。
頂点シェーダもフラグメントシェーダも単なるテキストではありますので、以下のようにHTML内に埋め込む事ができます:
シェーダはHTMLに埋め込める <script id="vtxshader" type="x-shader/x-vertex">
// ここに頂点シェーダを書くのです
</script>
<script id="frgshader" type="x-shader/x-fragment">
// ここにフラグメントシェーダを書くのです
</script>
typeを定義するのは、これをJavaScriptとして解釈されなくするためです。慣例的に上のようなtypeにするようですが、多分そうでなくても動きます。
○ 頂点シェーダ
WebGLのシェーダプログラムは「GLSL」というシェーダ用のプログラム形式で書きます。今回は「板ポリゴンを世界に1枚投入する」という目的なので、次のようなシェーダになりました:
世界に板ポリゴンを1枚投下する頂点シェーダ <script id="vtxshader" type="x-shader/x-vertex">
attribute vec3 aPos;
attribute vec4 aColor;
uniform mat4 uWVP;
varying vec4 vColor;
void main( void ) {
vColor = aColor;
vec4 outPos = vec4( aPos, 1.0 ) * uWVP;
gl_Position = outPos / outPos.w;
}
</script>
マルペケですから、この頂点シェーダ、余すことなく説明しますよー。
まず最初にある「attribute」。これは頂点に含まれる要素、つまり座標とか頂点カラーなどを受け取る専用の変数を宣言します。この宣言をすると描画時に勝手に頂点の要素の情報が飛び込んできます。「vec3」はGLSLに定義されている3次元ベクトルです。aPosにはローカル空間にある頂点座標が入って来る予定でいます。「vec4」もGLSLが用意している4次元ベクトルです。aColorは頂点カラーがやって来るとしています。
「uniform」というのは頂点要素以外の値を受け取る変数を宣言する物です。「mat4」は4x4行列ですよーという意味で、uWVPは「World
View Projection」合成行列の頭文字です。WVP行列はローカル空間にある頂点を一気に「射影空間」というスクリーン座標の一歩手前くらいの位置まで変換してくれます。この行列自体はHTML内にあるupdate関数内で作成して頂点シェーダのuWVPに渡す手筈と言うわけです。
次の「varying」はフラグメントシェーダに渡したい値を格納する変数です。頂点シェーダ内に宣言している変数は、頂点シェーダだけでしか使えません。でもフラグメントシェーダには色々な値を渡したいのです。そういう時にvaring宣言をします。上の例では、頂点カラーをフラグメントシェーダにそのままパスするために使っています。
頂点シェーダのプログラム本体は必ずvoid main( void )関数の中に書きます。お約束ですから従います(^-^)。最初にvaryingで宣言したvColorに頂点カラーaColorをそのまま放り込んでいます。色についてはこれでおしまい。
次に座標の変換をしています。aPosは3次元ベクトルですが、このままだとWVP行列に掛け算できないので、vec4に変換しています。4成分目の「1.0」は実はとっても重要で、これが無いとワールド変換やビュー変換をしても座標の位置が動かなくなってしまいます(平行移動成分が足し算されないため)。もう一つ重要な事、ローカル頂点座標の「右」からWVP行列を掛け算しています。これ、極めて重要です。ここから「uWVP行列は行オーダーなんだ」という事がわかります。行オーダーというのは4x4行列の1行目~3行目が回転成分を、4行目が平行移動成分を表す行列という意味です。これはDirectXがデフォルトで採用している方式です。OpenGLは列オーダーを採用してきました。これは1列目~3列目が回転成分、4列目が並行移動成分となっている行列です。数学的には行オーダーと列オーダーは共に転置行列の関係になっています。今回は行オーダーを採用する事にしました。理由は私にとってなじんでいるスタイルだからだけです。絶対そうしなければならないという物ではありません(^-^)
最後のgl_Positionというのも極めて大切。この特別な変数は頂点シェーダの戻り値の一つとして認識され、フラグメントシェーダの入力値を計算するのに使われます。gl_Positionには「射影空間の頂点座標を入れる事」と決められています。で、上の例ではWVP行列で変換したoutPosの各成分をoutPos.wで割り算しています。これは射影空間にある頂点に「遠近感」を付けるためのとても大切な計算なんです。w成分には上の変換で奥行きの情報が格納されます。それで割る事によって、奥にある頂点座標が原点付近に近寄ってきます。これによって「遠近感がある」と感じる事ができるんです。
という事で、結局この頂点シェーダは「入力されてきた頂点カラーをそのままスルー、頂点座標はWVP行列で射影空間へ変換し、遠近感を付けて出力(gl_Position)」という事をしているだけなんです。
○ フラグメントシェーダ
世界に板ポリゴンを1枚投下するフラグメントシェーダ precision mediump float;
varying vec4 vColor;
void main( void ) {
gl_FragColor = vColor;
}
頂点シェーダに比べて今回のフラグメントシェーダは大変にシンプルで、頂点シェーダで渡されてきた頂点カラーをそのまんま出力しています。「percision
mediump float;」という一文は、無くてもフラグメントシェーダ自体は動きます。この1行はシェーダ内計算の「精度」を設定しているんです。シェーダ計算はハードウェアのパワーをガンガン使うのですが、一般的なハードウェアは単精度浮動小数点(float)で計算を行います。上の宣言が無いとこれを倍精度(double)として計算しようとするので、計算負荷が高くなってしまいます。それを防ぐのがこの1行というわけ。
varyingは頂点シェーダで出てきたものですが、フラグメントシェーダで使うと「頂点シェーダから渡される値を受ける変数」という意味に変わります。この時の変数名は頂点シェーダときっちり一緒にしないと値が飛び込んできません。フラグメントシェーダもmain関数内に本体を記述します。上の例は…見たまんまです。gl_FragColorというのがフラグメントシェーダの出力になっていて、ここには画面に描画したいピクセルカラーを4次元ベクトルで指定します(普通はRGBAの順かな)。
これで簡単な頂点シェーダとフラグメントシェーダのGLSLコードが出来ました。次にこのコードを読み込んであげる必要があります。
④ シェーダをコンテキストにセットする
再びHTLM内の本体に戻ってきました。③で作成したシェーダをコンテキストに設定します。これには、んーまぁ結構な手順を要します。順を追って行きましょう。
上のシェーダはテキストのプログラムです。3Dな物を描画しようとした時に、このプログラムをJavaScriptよろしくインタプリタで解釈しながら描画していたのでは遅過ぎて使い物になりません。そのため、シェーダプログラムは必ず「コンパイル」されます。コンパイルする事でハードウェアが解釈できる超速なコードになり、描画もハードウェアの恩恵に授かれるようになるわけです。
シェーダをコンパイルする具体的な手順は、
・ シェーダテキストをJavaScriptの文字列として取得
・ シェーダを格納するシェーダオブジェクトを作成
・ シェーダオブジェクトにシェーダ文字列を流し込む
・ シェーダオブジェクトをコンパイル
・ コンパイルが成功したかチェック
となります。JavaScript側のプログラムはこんな感じです:
頂点シェーダをコンパイル // canvasからコンテキストを取得する
var canvas = document.getElementById("canvas");
var glc = canvas.getContext("webgl") || canvas.getContext("experimental-webgl");
// 頂点シェーダを読み込んでコンパイル
var shaderSrc = document.getElementById("vtxshader").text;
var vshader = glc.createShader( glc.VERTEX_SHADER );
glc.shaderSource( vshader, shaderSrc );
glc.compileShader( vshader );
if ( !glc.getShaderParameter( vshader, glc.COMPILE_STATUS ) ) {
var str = glc.getShaderInfoLog( vshader );
window.alert( "頂点シェーダエラー:\n" + str );
}
shaderSrcには頂点シェーダの文字列がそのまま流し込まれます。これはWebGLではなくてDOMのお話です。
gloc.createShader関数は引数に指定した空のシェーダオブジェクトを作ってくれます。上の例ではglc.VERTEX_SHADERというフラグを渡していますので、頂点シェーダ用のシェーダオブジェクトが作られるわけです。
空っぽのシェーダオブジェクトにシェーダテキストを流し込んでいるのが次のglc.shaderSource関数です。この段階ではただ流し込んでいるだけです。
続くglc.compileShader関数でシェーダオブジェクトを初めてコンパイルしてチョッ速なコードに内部で変換します。
if文の中にあるglc.getShaderParameter関数は、シェーダ内から色々なパラメータを取得できる関数ですが、この第2引数にglc.COMPILE_STATUSを渡すと、シェーダオブジェクトがコンパイルに成功したかどうかを判定してくれます。成功すれば素通りですが、失敗した場合はif文の中に突入します。
glc.getShaderInfoLog関数にコンパイルに失敗したシェーダオブジェクトを渡すと、具体的にどこが間違っていたかコンパイルエラーの情報を文字列で返してくれます。上の例ではそれをアラートウィンドウに表示させています。これ、物凄く便利です(^-^)
手順がやや多い感じがしますが、やっている事は単純です。
フラグメントシェーダについても、これと全く同じ手順でコンパイルします:
フラグメントシェーダをコンパイル // フラグメントシェーダを読み込んでコンパイル
shaderSrc = document.getElementById("frgshader").text;
var fshader = glc.createShader( glc.FRAGMENT_SHADER );
glc.shaderSource( fshader, shaderSrc );
glc.compileShader( fshader );
if ( !glc.getShaderParameter( fshader, glc.COMPILE_STATUS ) ) {
var str = glc.getShaderInfoLog( fshader );
window.alert( "フラグメントシェーダエラー:\n" + str );
}
頂点シェーダとの違いは上の太文字の箇所だけです。
このコンパイル作業によって2つのシェーダオブジェクト(vshader, fshader)が出来ます。最後に、これら2つのシェーダを結びつけた一つの「シェーダプログラム」を作ります。それには、
シェーダプログラムを作成 // シェーダプログラムを作る
var program = glc.createProgram();
glc.attachShader( program, vshader );
glc.attachShader( program, fshader );
glc.createProgram関数で空のシェーダプログラムを作成し、glc.attackShaderで頂点シェーダ、フラグメントシェーダをこの順でアタッチ(登録)していきます。最終的に使うのはこの「シェーダプログラム」です。この作業によって、ようやくコンパイル済みの超速シェーダコードを扱えるようになるわけです。ふぅ~~~(^-^;;
さ、次はモデルのお話ですよ。
⑤ ポリゴンの情報を作る
描く人の方はそれなりに整いましたので、今度は「描く物」のお話です。今回の目的は「板ポリ1枚を世界に投下」です。描く物とはその板ポリに他なりません。板ポリ(ポリゴン)は複数の頂点で構成されるのは言わずもがなです。ポリゴンを作るというのは頂点を作るという事になります。
頂点の情報と言うのは巨大なデータです。なので、これもJavaScriptの土俵でインタプリタ的に読み込みや解釈をしていたのでは全く使い物になりません。そこで、頂点の情報もハードウェアが解釈できる物に格納してあげる事になります。
まず、元となるデータはJavaScript上の配列として用意します。今回は板ポリ1枚なので、頂点座標の配列を次のように用意しました:
頂点座標配列を用意 // 頂点座標配列
var coords = [
-1.0, 0.0, 0.0,
0.0, 1.0, 0.0,
1.0, 0.0, 0.0,
];
XY平面上に張り付いている小さなポリゴンですね。この配列にある座標データをWebGLが扱える超速なバッファに格納します。それが次のコードです:
頂点座標バッファを作成して格納 var coordBuf = glc.createBuffer();
glc.bindBuffer( glc.ARRAY_BUFFER, coordBuf ); // バッファをセットして
glc.bufferData( glc.ARRAY_BUFFER, new Float32Array(coords), glc.STATIC_DRAW ); // 配列を流し込む
まずglc.createBuffer関数で空っぽの頂点バッファ(超速のバッファ)を用意します。次にそのバッファをglc.bindBuffer関数で一度コンテキストにセットしています。第1引数は「配列バッファですよ」と教えています。頂点座標データをバッファにコピーしているのが3行目。glc.bufferData関数を使います。第1引数が「配列バッファですよ」宣言、第2引数で単精度浮動小数点な配列を作り、そこに頂点座標配列をそのまま流し込んでいます。第3引数は「このバッファは一度セットしたら中身を書き変えませんよ」という宣言です。これにより、固定バッファとしてより高速に扱ってくれます。
今回の頂点シェーダには「頂点カラー」もありましたね。頂点カラーも全く同じような手順でバッファに格納します:
頂点カラーバッファを作成して格納 // 頂点カラーバッファ作成
var colors = [
1.0, 0.0, 0.0, 1.0,
1.0, 0.0, 0.0, 1.0,
1.0, 0.0, 0.0, 1.0
];
var colorBuf = glc.createBuffer();
glc.bindBuffer( glc.ARRAY_BUFFER, colorBuf );
glc.bufferData( glc.ARRAY_BUFFER, new Float32Array( colors ), glc.STATIC_DRAW );
頂点座標が3次元ベクトルなのに対して、頂点カラーは4次元ベクトルで定義する事に注意して下さい。後は何にも変わりません(^-^)。WebGLではこのように、頂点の各要素のバッファを別々に用意します。
さ、描画まであと一息です。
⑥ ベクトル・行列計算が待っていた!(涙)
描画する人(シェーダ)そして描画する物(頂点バッファ)も用意しました。後はこれらをコンテキストに流し込んで描画するだけなのですが、その前に「頂点変換行列」という厄介者が待っていました。なんで厄介かって、JavaScriptには行列計算なんて用意されている訳ないからです。WebGLにもそういう物はありません!なので全部用意する必要があるんです。行列演算をしてくれるライブラリは世の中にあります。Webで検索すればきっと拾えます。ただ、一応ここでは必要最低限のものだけ自前で作る事にします。
えーと、では具体的にどういう事をする必要があるかと言うと、
・ ワールド変換行列を作る
・ ビュー変換行列を作る
・ 射影変換行列を作る
・ 行列を掛け算する
以上の物が必須です。そして、これらを行うにはさらに、
・ 3次元ベクトルの内積
・ 3次元ベクトルの外積
・ 3次元ベクトルの正規化(Normalize)
が必要になります。ここで「ぎゃーー」と言った人、脱落です。これも越えねばならない壁なのですよ(T-T)g
簡単な所で3次元ベクトルクラスVec3から作りましょうか。Vec3ベクトルはx,y,z成分を持って、内積、外積、正規化等のメソッドを持っています。こんな感じです:
OXMath.Vec3クラス var OXMath = function() {};
// 3次元ベクトル
OXMath.Vec3 = function(x, y, z) {
var me = this;
this.x = x || 0.0;
this.y = y || 0.0;
this.z = z || 0.0;
// 足し算
this.add = function( v ) {
return new OXMath.Vec3( me.x + v.x, me.y + v.y, me.z + v.z );
}
// 引き算
this.sub = function( v ) {
return new OXMath.Vec3( me.x - v.x, me.y - v.y, me.z - v.z );
}
// 長さ
this.len = function() {
return Math.sqrt( x * x + y * y + z * z );
}
// 正規化
this.normal = function() {
var n = me.len();
if ( n != 0.0 )
return new OXMath.Vec3( x / n, y / n, z / n );
return new OXMath.Vec3();
}
// 外積
this.cross = function( r ) {
return new OXMath.Vec3(
y * r.z - z * r.y,
z * r.x - x * r.z,
x * r.y - y * r.x
);
}
// 内積
this.dot = function( r ) {
return x * r.x + y * r.y + z * r.z;
}
}
もう一つきっつい事がありました。JavaScriptは演算子のオーバーロードなんて概念も無いので、足し算や引き算もメソッドです。
続いて4x4行列。最低限な実装だけですがこんな感じです:
OXMath.Mat4x4クラス // 4x4行列
OXMath.Mat4x4 = function() {
var me = this;
this.m11 = 1.0; this.m12 = 0.0; this.m13 = 0.0; this.m14 = 0.0;
this.m21 = 0.0; this.m22 = 1.0; this.m23 = 0.0; this.m24 = 0.0;
this.m31 = 0.0; this.m32 = 0.0; this.m33 = 1.0; this.m34 = 0.0;
this.m41 = 0.0; this.m42 = 0.0; this.m43 = 0.0; this.m44 = 1.0;
// 配列として取得
this.ary = function() {
return [
me.m11, me.m12, me.m13, me.m14,
me.m21, me.m22, me.m23, me.m24,
me.m31, me.m32, me.m33, me.m34,
me.m41, me.m42, me.m43, me.m44
];
}
// 転置配列として取得
this.aryT = function() {
return [
me.m11, me.m21, me.m31, me.m41,
me.m12, me.m22, me.m32, me.m42,
me.m13, me.m23, me.m33, me.m43,
me.m14, me.m24, me.m34, me.m44
];
}
// 掛け算
this.mul = function( m1 ) {
var r = new OXMath.Mat4x4();
r.m11 = me.m11 * m1.m11 + me.m12 * m1.m21 + me.m13 * m1.m31 + me.m14 * m1.m41;
r.m12 = me.m11 * m1.m12 + me.m12 * m1.m22 + me.m13 * m1.m32 + me.m14 * m1.m42;
r.m13 = me.m11 * m1.m13 + me.m12 * m1.m23 + me.m13 * m1.m33 + me.m14 * m1.m43;
r.m14 = me.m11 * m1.m14 + me.m12 * m1.m24 + me.m13 * m1.m34 + me.m14 * m1.m44;
r.m21 = me.m21 * m1.m11 + me.m22 * m1.m21 + me.m23 * m1.m31 + me.m24 * m1.m41;
r.m22 = me.m21 * m1.m12 + me.m22 * m1.m22 + me.m23 * m1.m32 + me.m24 * m1.m42;
r.m23 = me.m21 * m1.m13 + me.m22 * m1.m23 + me.m23 * m1.m33 + me.m24 * m1.m43;
r.m24 = me.m21 * m1.m14 + me.m22 * m1.m24 + me.m23 * m1.m34 + me.m24 * m1.m44;
r.m31 = me.m31 * m1.m11 + me.m32 * m1.m21 + me.m33 * m1.m31 + me.m34 * m1.m41;
r.m32 = me.m31 * m1.m12 + me.m32 * m1.m22 + me.m33 * m1.m32 + me.m34 * m1.m42;
r.m33 = me.m31 * m1.m13 + me.m32 * m1.m23 + me.m33 * m1.m33 + me.m34 * m1.m43;
r.m34 = me.m31 * m1.m14 + me.m32 * m1.m24 + me.m33 * m1.m34 + me.m34 * m1.m44;
r.m41 = me.m41 * m1.m11 + me.m42 * m1.m21 + me.m43 * m1.m31 + me.m44 * m1.m41;
r.m42 = me.m41 * m1.m12 + me.m42 * m1.m22 + me.m43 * m1.m32 + me.m44 * m1.m42;
r.m43 = me.m41 * m1.m13 + me.m42 * m1.m23 + me.m43 * m1.m33 + me.m44 * m1.m43;
r.m44 = me.m41 * m1.m14 + me.m42 * m1.m24 + me.m43 * m1.m34 + me.m44 * m1.m44;
return r;
}
}
難しい事は何もしていないのですが、とにかく計算量が多くて記述が面倒なんですよね…。ちなみに、OXMathのMat4x4行列はデフォルトで単位行列です(^-^)。
後はヘルパー関数としてビュー行列と射影変換行列を作る関数がこちら:
ビュー行列、射影変換行列 // Degree -> Radian
OXMath.toRad = function( deg ) {
return deg / 180.0 * 3.14159265358979;
}
// LookAtでビュー行列作成
OXMath.lookAtLH = function( eye, at, up ) {
var zaxis = at.sub( eye ).normal();
var xaxis = up.cross( zaxis ).normal();
var yaxis = zaxis.cross( xaxis );
var m = new OXMath.Mat4x4();
m.m11 = xaxis.x; m.m12 = yaxis.x; m.m13 = zaxis.x;
m.m21 = xaxis.y; m.m22 = yaxis.y; m.m23 = zaxis.y;
m.m31 = xaxis.z; m.m32 = yaxis.z; m.m33 = zaxis.z;
m.m41 = -xaxis.dot( eye );
m.m42 = -yaxis.dot( eye );
m.m43 = -zaxis.dot( eye );
return m;
}
// パースペクティブ行列作成
OXMath.perspLH = function( fovY, aspect, zn, zf ) {
var yScale = 1.0 / Math.tan(fovY/2)
var xScale = yScale / aspect;
var m = new OXMath.Mat4x4();
m.m11 = xScale;
m.m22 = yScale;
m.m33 = zf / ( zf - zn );
m.m34 = 1.0;
m.m43 = -zn * zf / ( zf - zn );
m.m44 = 0.0;
return m;
}
これだけあれば何とかなります(^-^;。
⑦ 描画へ!
さ、いよいよ描画部分です。まずはWVP行列を作りましょうか。これは上のヘルパー群があれば簡単です:
ビュー行列、射影変換行列 // 変換行列作成
var world = new OXMath.Mat4x4();
var view = OXMath.lookAtLH(
new OXMath.Vec3( 0.0, 0.0, -5.0 ),
new OXMath.Vec3( 0.0, 0.0, 0.0 ),
new OXMath.Vec3( 0.0, 1.0, 0.0 )
);
var proj = OXMath.perspLH( OXMath.toRad(30.0), 1.0, 0.01, 100.0 );
var wvp = world.mul(view).mul(proj);
world行列は単位行列、つまりローカル空間の頂点座標がそのままワールド座標になります。次のview行列はLookAt形式で作成しています。第1引数がカメラの位置、第2引数が注視点、第3引数が空ベクトルです。上のカメラはZ軸上のz=-5.0の位置にあるわけです。射影変換行列projは、OXMath.perspLH関数で作ります。第1引数は画角をラジアン角で指定します。第2引数はアスペクト比です。今回canvasは幅も高さも480なので、アスペクト比は1,0です。第3引数は近平面までの距離で0.01にしています。第4引数は遠平面までの距離で、こちらは100.0に設定。最後にこれらの行列をworld*view*projの順で掛け算してWVP行列の完成です。
ここからが最後の壁、シェーダをコンテキストに設定する箇所です。ゆっくり説明していきます。まず、コンテキストに先に作成したシェーダプログラムを設定します:
コンテキストにシェーダプログラムをセット glc.useProgram( program );
続いて頂点シェーダに設定されているattributeとuniformを表す変数を取得します:
頂点シェーダへの入力引数を取得 var aPos = glc.getAttribLocation( program, "aPos" );
var aColor = glc.getAttribLocation( program, "aColor" );
var uWVP = glc.getUniformLocation( program, "uWVP" );
頂点シェーダでattributeとしてaPos、aColor、uniformとしてuWVPという3つの変数を宣言しましたね。それらを表す変数をglc.getAttribLocation関数、glc.getUniformLocation関数でそれぞれ取得しています。取得して何をするか?これらの変数に頂点座標バッファと頂点カラーバッファをくっつけてあげるんです:
各バッファとシェーダ引数を繋ぐ // 座標
glc.bindBuffer( glc.ARRAY_BUFFER, coordBuf );
glc.vertexAttribPointer( aPos, 3, glc.FLOAT, false, 0, 0 );
// カラー
glc.bindBuffer( glc.ARRAY_BUFFER, colorBuf );
glc.vertexAttribPointer( aColor, 4, glc.FLOAT, false, 0, 0 );
// 行列
glc.uniformMatrix4fv( uWVP, false, wvp.ary() );
まずglc.bindBuffer関数でコンテキストに頂点バッファを設定します。次にglc.vertexAttribPointer関数でそのバッファと頂点シェーダ引数とを結びつけます。
第1引数は結び付けたい頂点シェーダ引数です。
第2引数はベクトルの次元数になります。上の例の頂点座標バッファの場合は3次元ベクトルだったので「3」が設定されています。
次の第3引数はデータの「型」を指定します。通常使う値はまずglc.FLOATでしょうね(たま~にint型もあります)。
第4引数は「正規化するか?」をboolで指定します。ここで言う正規化というのは、整数値を小数点にするかどうかという意味なんです。このフラグは第3引数で整数型を指定した場合にのみ作用します。なので浮動小数点の場合はfalseでOK。
第5引数は「ストライド(stride)」です。これは頂点バッファのひと固まり、頂点座標で言えば3次元ベクトルのサイズを指定するのですが、0にすると第2引数と第3引数の情報から自動的に計算してくれます。ここに数値を入れるというのは、ひと固まりのサイズが異なる時です。例えば1頂点を4次元ベクトルで表現しているけども頂点シェーダが3次元ベクトルを要求する場合などです。この場合はここに12(float型は4バイト×3成分)が入ります。まぁ、特殊な事をしなければ0になります。
最後の第6引数は頂点バッファの読み始めのオフセットサイズを指定します。配列の最初に何か入っている場合はここでオフセットします。これも配列の最初から頂点情報が並んでいるならば0で固定です。
上の例では頂点座標バッファ(coordBuf)そして頂点カラーバッファ(colorBuf)をそれぞれaPosとaColorに結び付けています。これでattributeについてはOK。
一方のuniformの方ですが、これは各型毎に関数が細かく分かれています。今は4x4行列であるWVP行列を渡したいのでglc.uniformMatrix4fv関数を用います。
第1引数には対象となるシェーダ引数を指定します。
第2引数は行列を転置するかを指定します。今は転置の必要が無いのでfalseとしています。
第3引数に4x4行列となる配列を渡します。これは実際には浮動小数点が16個並んだ配列です。
このちょっと面倒くさい結び付けを行って始めてデータが頂点シェーダに流れます。最後にコンテキストに使用する頂点シェーダ引数のattirubuteを教えてあげます:
使用するattributeを指定 glc.enableVertexAttribArray( aPos );
glc.enableVertexAttribArray( aColor );
教えてあげるにはglc.enableVertexAttribArray関数を使います。上の例では頂点シェーダに指定した2つのattribute両方とも使うと宣言していますが、例えばaColorの方をコメントアウトすると、頂点カラーが使われなくなります。その場合頂点カラーの成分は0になってしまいます。つまり真っ黒。aPosの方をコメントアウトすると、もちろんポリゴンは描画されません。
さ!これですべての設定が終わりました。最後の最後に、
描画! glc.drawArrays( glc.TRIANGLES, 0, 3 );
とglc.drawArrays関数で描画を指示します。
第1引数にはプリミティブタイプを指定します。今は三角形ポリゴン1枚なのでglc.TRIANGLESフラグを指定します。
第2引数は頂点の描画開始番号を指定します。例えば頂点バッファに複数のモデルをいっぺんに突っ込む事もできます。その場合、2番目やその次のモデルなどは頂点バッファの途中からスタートさせないといけません。そういう場合にここにオフセット頂点数を指定します。
第3引数は描画する頂点の数です。今は当然「3」です。
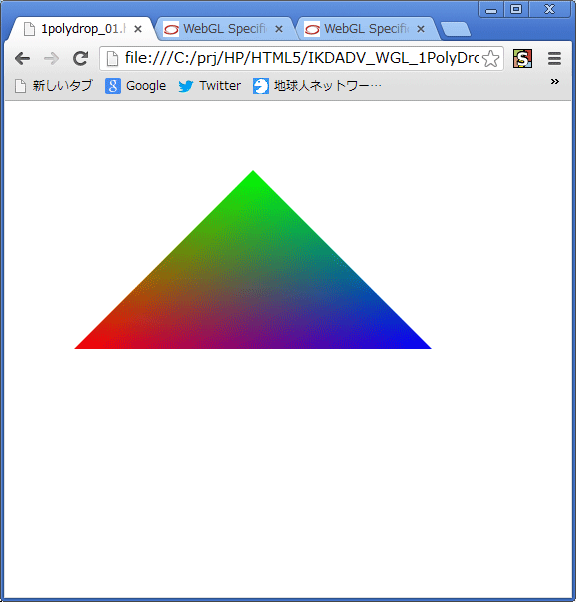
以上の諸命令をコールすると、次のようなカラフルな三角ポリゴンがブラウザ上に1枚表示されます:
うひょー(^-^)/
このポリゴンは2Dではなくて3Dなので、もちろん回したりもできます。カメラの位置を変えれば別の見え方をしますし、射影変換行列を変えれば遠近感の解釈も変わります。ポリゴンを1枚出せれば、それを組み合わせて複雑なモデルも表せる事になります。
こんな感じでWebGLを用いてブラウザに3Dな物を表示できるようになりました。ただ、さすがにこの流れをあらゆるモデル描画にまともに採用するのは厳しいですね。モデル情報も読み込む必要がありますが、具体的にどうするか?シェーダもモデルによって全く違いますから、HTMLに埋め込むわけにもいきません。ズドン!っと通したコードを使いやすく再利用しやすい形にする課題が山積しているわけです。ちょっとずつ考えて行きましょう。