その11 波:頂点波に環境マップ+フレネル反射を反映させる
頂点の座標を直接変更して波を表現する頂点波。前章までで頂点波としてsin波やゲルストナー波を起こす事が出来るようになりました。ただライティングが適当なので、水の波と言うよりマットな平面がうねっている見た目になっていました。これは「水を水たらしめる要素」を組み込む事によってどんどん改善していきます。
水が水のように見える要素には様々な物がありますが、その一つに「透過と反射」があります。水と言ったらまず誰もが「透明」をイメージしますよね。水槽内の魚が見えるのは水が透明だからです。では人はなぜ透明な物を「透明だ」と判断出来るのか?それは言わずもがなですが「透明物の向こうにある物が見える」からです。でも良く考えてみて下さい。深い海の底は海面からは見えません。水の向こうが見えないのですから「深い海は透過していない」と言えてしまいます。でも、私たちは深い海の映像を見たら「あ~水だ」と認識します。透過性以外にも水を感じさせる要素があるという事です。
透過と表裏一体な物として「反射」があります。水面を観察すると周りの景色を反射させているのが分かります。しかもその反射は一様ではありません。水面を真横近くから見るとかなり強く景色を反映させますが、水面を真上に近い角度で見ると周りの景色はあまり見えず、水の色が強く見えます。水面に対してみる角度によって反射の度合いが異なるんです。これを「フレネル反射」と言います。このフレネル反射があると、人は水を水っぽく感じるんです。
という事で、この章では頂点波に周りの景色を移し込み、フレネル反射させてみようと思います。
① フレネル反射の原理
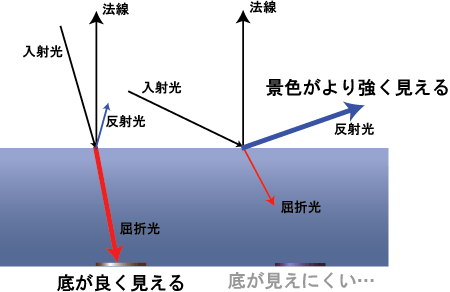
フレネル反射については古い記事になりますがマルペケでも一度取り上げています(プログラマブルシェーダ編その7「斜めから見ると底が見えない水面(フレネル反射)」)。なので細かい事はリンク先の記事に譲りますが、イメージ図を再掲します:
私達の目は飛び込んで来た光を認識します。その光は光源から発せられると考えます。上の図で言うと「入射光」がそれに該当します。光が水面に当たると、その光はざっくり2つの方向に分かれます。一つは「屈折光」で入射角に対してある一定の角度で折れ曲がり、そのまま水中を直進していきます。屈折光が水底に届き、再び反射して水面から飛び出て、それが私達の目に届いた時、初めて私たちは「水底が見えた」と認識できるんです。もう一つは「反射光」です。これは単純に入射角と等しい角度で跳ね返る光です。私達の目が反射光を捉えると、脳はそれを「周りの景色が映り込んでいる」と認識します。
屈折光と反射光の強さは、入射光の角度と媒体によってある程度決まります。上図のように入射角が大きい(左図)と屈折光が強くなり反射光は弱くなります。逆に入射角が浅い(右図)と反射光が強くなり屈折光は弱くなります。そしてある入射角以下になると屈折光がほぼ起こらなくなる「全反射」という状態になります。
この入射角度に対する屈折光と反射光の割合をモデル化したのが「フレネル反射」で、以下の式で表現されます:
Rは入射光の反射率で1.0(100%)ならば全反射になります。逆に0.0だと完全透過(屈折光が100%)です。αは入射角度で、βは屈折角度です。で、この式を先のリンク先では「うりゃ~」っと変形して次のような式を導出しました:
n1は入射光が進んでいる媒体の屈折率、n2は入射光が突入しようとする媒体の屈折率です。媒体(空気とか水とか)の屈折率は良く知られています(Wikipedia:屈折率)。空気中を飛んで来た入射光が水に飛び込むのであれば、n1=1.000292、n2=1.3334なのでAは約0.7502です。Bは入射角度αのcos値で、これは入射光の方向ベクトル(-L)と法線Nの内積で一発です。この簡単なパラメータから反射率Rが計算出来てしまいます(^-^)
○ フレネルの式に関して
所で先のフレネルの式ですが、元式を掲載した2010年当時確かWikipediaにあった気がしたのですが、現在(2019.7)は見当たりません。よって現在出典元不明になっています。式の形と現在のWikipediaの説明から類推するに、sin側の2乗式は「s波」のエネルギーの反射率、tan側は「p波」のエネルギーの反射率になっています。それを足して2で割っているという事は、双方のエネルギー反射率の平均値を取っている事になります。出典が不明になってしまった現時点でこの式の厳密性は保証できないのでご注意ください。もしこの式が載っているサイトや書籍がありましたら是非教えて下さい m(_ _)m
② 深い海の色味とは
入射光が水に飛び込んだ時、その一部は屈折光となり水の中を突き進みます。もし水の透過度が高くて底が浅ければ、その光は水底に反射して再び水面から飛び出します。しかし通常その光は入射直後よりも弱くなっています。それは水の中で光が一定の割合で散乱してしまうためです。このため水底にある物は水深が深くなる程見えにくくなります。
水深が十分に深い場合、屈折光がどれほど強くても水底の物は見えません。反射光が起こらないように水面に対して垂直に見てもそれは同じです。では反射光0%で屈折光が見えない状態で目に見える色は何なのか?真っ黒でしょうか?でも私達は深い海を真上から見ても色味を感じています。何らかの光が目に飛び込んできているという事です。その目に感じている光の正体は「表面拡散反射光(ディフューズ)」です。ディフューズは面に当たる光の強さに比例してその表面の色を全方向に反射させると仮定します。反射光を取り除いた時、結果として私達は屈折光の強さに比例したディフューズ色を目に受ける事になります:
水面のディフューズ色をSDcとするなら、目に入ってくるディフューズ成分Dcは、
と計算出来る事になります。
では角度の浅い所はというと、屈折光による色味は減るのですが、フレネル反射の性質により代わりとして反射光が色濃く出てくるようになります。その反射率はR(α)なので、入射光の色味をLcとすると、Lc*R(α)が目に入る色味となります。よって、ある反射角度αの地点での総合的な色味Cは、
と算出できる事がわかります。線形補間ぽい感じですよね。
水のディフューズ色が何色なのか?という根本的な所ですが、これは多くは表現の問題なのである程度は目検討でも良いのかなと思うのですが、Wikipediaの「水の青」によると十分に長いパイプに純粋を満たし白色光源を当てて観察すると「ターコイズブルー」に見えるそうです。ターコイズブルーは以下のような色です:
RGB = ( 0, 183, 206 )
#00B7CE
身の回りの水は純粋では無いので、多少これよりはちょっとだけくすんだ色味になるのかなと思いますが、まぁ表現の問題です(^-^;。
③ 環境マップを反映させる
頂点波は水面のある地点での法線が分かっているので、環境マップを適用させる事が出来ます。Unityの場合環境マップを適用するのはかなり簡単です。まず天球となる「キューブマップ」を作ります。これは上下左右前後6面を撮影した特殊なテクスチャを用意し、プロジェクトウィンドウ内で右クリックし、[Create]→[Legacy]→[Cubemap]を選択します。適当な名前を付けたら、最初に[Face Size]を決めてから対応する所にテクスチャをドラッグしていきましょう:
作成したCubemapをシェーダで扱うには以下のようにします:
Properties
{
...
_Cubemap( "Cubemap", Cube ) = ""{} // Cubeテクスチャ設定
}
SubShader
{
Pass
{
UNITY_DECLARE_TEXCUBE( _Cubemap ); // キューブテクスチャを変数として定義
....
v2f vert (appdata v)
{
v2f o;
// ワールド頂点位置を保持
o.vertexW = mul( unity_ObjectToWorld, v.vertex );
....
}
fixed4 frag (v2f i) : SV_Target
{
....
// カメラの方向ベクトル
float3 fromVtxToCameraW = normalize( _WorldSpaceCameraPos - i.vertexW.xyz );
// 反射ベクトル
float3 reflectDirW = reflect( -fromVtxToCameraW, normalW );
// 反射ベクトルの先にあるキューブマップをフェッチ
float4 envColor = UNITY_SAMPLE_TEXCUBE( _Cubemap, reflectDirW );
....
}
キューブマップに関わる所だけを抜き出してみました。まずPropertiesでCubeを指定しキューブマップを設定できるようにします。それをUNITY_DECLARE_TEXCUBEマクロで変数として扱えるようにします。頂点シェーダではフラグメントシェーダで必要となるワールド頂点位置を算出・保持します。フラグメントシェーダでは反射ベクトルを求めるために頂点位置からカメラまでのベクトル(fromVtxToCameraW)を算出してreflect関数に法線と一緒に渡します。reflect関数は入射ベクトルを必要とするためカメラまでのベクトルを反転させています。最後に求めた反射ベクトルの先にある環境マップの色をUNITY_SAMPLE_TEXCUBEマクロを通して取得しています。こうプロセスを言葉にすると何とも長たらしいですが(^-^;、プログラムは至ってシンプルです。
フェッチした環境マップの色は反射率Rを掛けて、水の地の色に足し込む事でディフューズ色が決まります。後は法線とライトのベクトル関係から陰影を付け、スペキュラを入れると水っぽさが増します。
④ フレネル反射と環境マップ入り波シェーダ
ここまでの理屈を踏まえたシェーダを書いてみます:
// ゲルストナー波(フレネル反射と環境マップ)
Shader "IKD/GerstnerWave"
{
Properties
{
_MainTex ("Texture", 2D) = "white" {}
_BaseColor ("Base color", Color ) = (1.0, 1.0, 1.0, 1.0 )
_Cubemap( "Cubemap", Cube ) = ""{}
_t("Time(sec)", float ) = 0.0
}
SubShader
{
Tags {
"RenderType"="Opaque"
"LightMode"="ForwardBase"
}
LOD 100
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
// make fog work
#pragma multi_compile_fog
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
UNITY_FOG_COORDS(1)
float4 vertex : SV_POSITION;
float4 vertexW : TEXCOORD2;
float3 normalW : TEXCOORD3;
};
float _t;
sampler2D _MainTex;
float4 _MainTex_ST;
float4 _BaseColor;
UNITY_DECLARE_TEXCUBE( _Cubemap );
// ゲルストナー波
void gerstnerWave( in float3 localVtx, float t, float waveLen, float Q, float R, float2 browDir, inout float3 localVtxPos, inout float3 localNormal ) {
browDir = normalize( browDir );
const float pi = 3.1415926535f;
const float grav = 9.8f;
float A = waveLen / 14.0f;
float _2pi_per_L = 2.0f * pi / waveLen;
float d = dot( browDir, localVtx.xz );
float th = _2pi_per_L * d + sqrt( grav / _2pi_per_L ) * t;
float3 pos = float3( 0.0, R * A * sin( th ), 0.0 );
pos.xz = Q * A * browDir * cos( th );
// ゲルストナー波の法線
float3 normal = float3( 0.0, 1.0, 0.0 );
normal.xz = -browDir * R * cos( th ) / ( 7.0f / pi - Q * browDir * browDir * sin( th ) );
localVtxPos += pos;
localNormal += normalize( normal );
}
v2f vert (appdata v)
{
v2f o;
o.vertexW = mul( unity_ObjectToWorld, v.vertex );
float3 oPosW = float3( 0.0, 0.0, 0.0 );
float3 oNormalW = float3( 0.0, 0.0, 0.0 );
gerstnerWave( o.vertexW, _t + 2.0, 0.6, 0.8, 0.5, float2( 0.2, 0.3 ), oPosW, oNormalW );
gerstnerWave( o.vertexW, _t , 1.4, 0.8, 0.5, float2( -0.4, 0.7 ), oPosW, oNormalW );
gerstnerWave( o.vertexW, _t + 3.0, 1.6, 0.8, 0.5, float2( -0.4, -0.4 ), oPosW, oNormalW );
gerstnerWave( o.vertexW, _t , 2.4, 0.8, 0.5, float2( -0.3, 0.6 ), oPosW, oNormalW );
o.vertexW.xyz += oPosW;
// 座標変換
o.vertex = mul( UNITY_MATRIX_VP, o.vertexW );
o.uv = TRANSFORM_TEX( v.uv, _MainTex );
o.normalW = normalize( oNormalW );
UNITY_TRANSFER_FOG( o, o.vertex );
return o;
}
// フレネル反射率を算出
float fresnel( in float3 toCameraDirW, in float3 normalW, in float n1, in float n2 ) {
float A = n1 / n2;
float B = dot( toCameraDirW, normalW );
float C = sqrt( 1.0 - A * A * ( 1.0 - B * B ) );
float V1 = ( A * B - C ) / ( A * B + C );
float V2 = ( A * C - B ) / ( A * C + B );
return ( V1 * V1 + V2 * V2 ) * 0.5;
}
fixed4 frag (v2f i) : SV_Target
{
// sample the texture
fixed4 col = tex2D(_MainTex, i.uv);
float3 normalW = normalize( i.normalW );
float3 toLightDirW = normalize( _WorldSpaceLightPos0.xyz );
float3 waterColor = _BaseColor;
// フレネル反射率算出
// 頂点座標からカメラへのレイと法線
float3 fromVtxToCameraW = normalize( _WorldSpaceCameraPos - i.vertexW.xyz );
float R = fresnel( fromVtxToCameraW, normalW, 1.000292, 1.3334 ); // 反射率
// 環境マップサンプル
float3 reflectDirW = reflect( -fromVtxToCameraW, normalW );
float4 envColor = UNITY_SAMPLE_TEXCUBE( _Cubemap, reflectDirW );
// ディフューズ色
// 水の色と環境マップを合成 → ライトとの角度で陰影
float3 srcColor = waterColor * ( 1.0 - R ) + envColor.rgb * R;
float diffusePower = dot( normalW, toLightDirW );
float3 diffuseColor = srcColor * diffusePower;
// スペキュラ
float3 halfDirW = normalize( toLightDirW + fromVtxToCameraW );
float3 specularColor = pow( max( 0.0, dot( halfDirW, normalW ) ), 30.0f );
col.rgb = diffuseColor + specularColor * 0.75f;
UNITY_APPLY_FOG( i.fogCoord, col );
return col;
}
ENDCG
}
}
}
フラグメントシェーダ内が今回のコアです。視線のベクトルと法線からフレネル反射率(R)を求め、環境マップの強度にしています。水の地の色(waterColor)はその反転強度になります。後は通常のディフューズ強度とスペキュラカラーを合成して終わりです。
上のシェーダをUnityで動かしてみると次のような動画の見た目になりました:
前章よりもより波感が増していますよね。