その2 TLSFメモリアロケータ
~ フラグメント耐性高速メモリアロケータ ~
C++はnewとdeleteで特定のメモリにオブジェクトを作ります。デフォルトのnewは様々な状況に対応するために速度よりも汎用性と安全性に重点が置かれています。そのためnewはかなり遅い処理となっています。
ゲームプログラムは恐ろしい回数のnewとdeleteが発生します。ですからnewが遅いというのは致命的です。もう一つ、Windows OSのnewのアルゴリズムはフラグメンテーション(断片化)が起こりにくいように取り扱ってくれるのですが、コンシューマ機では皆無です。ですから、メモリを限界まで効率良く使うためにも断片化対策は必要になります。もう一つ、メモリには「メモリリーク」という爆弾が常につきまといます。デフォルトのnewではメモリリークの発見はほぼ無理です。ちゃんとゲームを作るのであれば、これも独自に考える必要があります。結局「メモリ管理はいずれ独自に作らないといかん!」というわけです。
メモリの確保と解放を管理するメモリアロケータは世の中にたっくさんあります。論文も山ほど。それだけ重要だという事ですが、その中でTLSFメモリアロケータという物があります。出典は「Dynamic storage allocation for real-time embedded systems (M. Masmano, I. Ripoll, and A. Crespo). Real-Time Systems Symposium, Work-in-Progress Session. Cancun, Mexico, December 2003.」で、実はホームページがあります(TLSF)。このサイトに論文が公開されています。
メモリアロケータでは「超大なメモリ空間の中で要求された空きメモリをいかに速く見つけるか」がパフォーマンスに大変影響します。TLSF(Two-Level Segregate Fit)メモリアロケータはこの検索スピードが非常に速いのが特徴です。ただ、実装はなかなかにして大変です。論文を読み読み、少しずつ頑張ってみます。
① 要求したサイズに「GoodFit」するメモリを2段階で探す
このアロケータのアルゴリズムは、例を使わないとうひゃーっと大混乱します。具体的に行きましょう。
ほとんどすべてのメモリアロケータは一塊の巨大なメモリブロックを最初に確保します。TLSFも同様です。今仮に4096バイトのメモリをごっそりと確保しているとして、TLSFに「140バイトのメモリを下さい」と頼んだとしましょう。TLSFはメモリ要求が来ると、そのサイズに見合う使用可能なメモリブロックを検索しに行きます。この時、2段階の検索が行われます。
まず第1段階では、要求されたサイズが格納できる2のべき乗サイズ幅を調べます。140がどのべき乗サイズに入るかは、この数字を2進数で見てみるとあっという間にわかります:
140 = 0000 0000 1000 1100
2進数にした140の最上位ビットは上の赤い1です。ここは10進数で言えば「128」。つまり140は128以上256未満である事がすぐにわかるわけです。これが「第1カテゴリー」となります。
続いて、この128から256の間を細かく分割します。高速化のためこれも2のべき乗個に分割します。例えば4分割するとしましょう。その場合128 / 4 = 32バイト単位で次のようなサブカテゴリーで分割されます:
第2段階カテゴリ(128-255) 128 ~ 159 160 ~ 191 192 ~ 223 224 ~ 255
ここから、140は黄色い範囲に入る事がわかります。この黄色い範囲を最速で見つけるのがTLSFのアルゴリズムです。それは後ほど。
さて、この範囲を見つけたら、次にこの範囲の「フリーブロックリスト」に余りがあるかをチェックします。フリーブロックリストというのは使用可能状態になっているメモリブロックが連なっているリストです。第2段階の各範囲には一つずつ、その範囲のメモリを格納可能なフリーブロックリストがくっついています。ここで重要なのが「格納可能な」という部分。例えば、ここに135バイト分のメモリブロックがぶら下がっていたとします。すると140バイトの要求に答えられません。こうなると、フリーリストにぶら下がっているメモリブロックが信用できなくなってしまいます。そして、毎回リンクリストを線形に辿って確保可能なメモリを探す作業になってしまいます。それではパフォーマンスはガタ落ちです。ですから、ここには159バイト以上の空き容量が確実にあるメモリブロックが並んでいないといかんわけです。
これは逆に言えば、フラグメントが確実に起こる事も示唆しています。128~159バイトのサイズが確実に入るというのは159バイト以上のブロックであるわけですから。パフォーマンスを稼ぐためにフラグメントを起こさないBestFitではなくソコソコに入るGoodFitを採用したのがTLSFです。「フラグメンテーションが起こる…ん~」と思われるかもしれませんが、ここに第2カテゴリの存在が大きく関わります。第2カテゴリはメモリサイズをさらに細かく分類しています。これにより、GoodFit性が増すため、過度のフラグメントが起こりにくくなります。
話を続けましょう。今は一番最初のまっ更な状態なので、この小さな範囲に所属している空きメモリブロックはありません(もっと巨大な4096バイトのフリーブロックが一つあるだけ)。よって、140バイトを程々に格納できそうなメモリブロックは無いという結果になります。
その場合どうするか?もっと大きなメモリブロックが無いか探します。真っ先に探すのは、自分が所属する第1段階のカテゴリですが、そこにも無ければより上のカテゴリを見に行きます。今はまっ更な状態からスタートしているので、一番大きなメモリブロックに欲しいフリーブロックが見つかるでしょう:
第1段階カテゴリ フリーリストがある? 32 - 64 × 64 - 128 × 128 - 256 × 256 - 512 × ... × ... × 4096 - 8192 ○(あった~!)
この格納可能なフリーブロックをTLSFではビット演算で高速で割り出してしまいます。その話も後ほど。現状では4096バイトの巨大なフリーメモリブロックが1つだけありますので、これが140バイトのメモリを格納する候補となります。
要求したサイズのメモリを確保できるフリーブロックを見つけたら、そのフリーブロックは「使用中」となります。ただ、高々140バイトを確保するために4096バイトのメモリブロックが丸々占有されるわけには行きません。そこで、そのフリーブロックが分割できるかを調べます。4096バイトのフリーメモリは140バイトの使用中ブロックと残り3956バイトのフリーブロックに分割できます。使用中メモリは要求者に返し、残った3965バイトのフリーブロックは新しい所属先のフリーブロックリストにくっつけます:
第1段階カテゴリ 第2カテゴリ 32 - 64 64 - 128 128 - 256 256 - 512 ... 2048 - 4096 2048 - 2559 2560 - 3071 3072 - 3583 3584 - 4095 4096 - 8192
上の赤い所に新しくフリーブロックがリストに追加される事になります(確実に格納可能なブロックであることに注目)。
② メモリの解放とフリーブロックのマージ
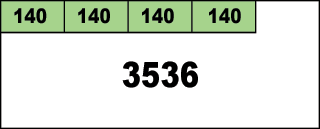
さて、同様に140バイトの要求が合計4回来た時のメモリの使用状況を見てみましょう:
ブロックの先頭から4つ確保されて、残りが3536バイトとなっています。ここから例えば「2番目のメモリがいらな~い」となったとしましょう。free関数やdeleteにポインタを指定する事でわかるように、通常メモリが不要になった時にはいらないメモリの先頭アドレスが削除する人に渡されるはずです。よって、TLSFにも2番目の140バイト分のメモリブロックの先頭アドレスが直接渡されます。
所で、例えば「削除してくれ~」と0x0042afc3というアドレスがTLSFに渡されたとします。しかし、上のように必要メモリだけを確保してしまうと、そのアドレスから「何バイトフリーにするべきか」がわかりません。貸す時には確かに140バイト切り出して貸出しましたが、どこにもそのサイズを記録していないからです。これでは、解放作業が出来ません。
そこで強烈に役に立つのが、前章で紹介した「Boundary Tagアルゴリズム」です。このアルゴリズムは上のように連続した不定長のブロック間をぴょんぴょん飛ぶ事ができます。それができるのは確保サイズを知っているためです。Boundary Tagは下図のように確保メモリの前に青い領域で表した固定サイズのヘッダー(前方タグ)があるため、解放したいと渡されたメモリのアドレスからブロックの先頭を簡単に計算できます:
解放作業自体は非常に単純で、使用可能フラグをおろします。このフラグを下ろしてしまえば、このメモリブロックはフリーブロックとなり、然るべきリスト([112-127]のブロック)に加えられる事になります。これで、1つの解放作業が終了します。
では、続いて3番目の140バイトも解放要求が来たとします。先と同じ事を考えれば、使用中フラグを下ろして、フリーリストに加える事になるかと思いきや、実はそうではありません。なぜか?下のメモリマップを御覧ください:
2番目と3番目は解放されています。しかし、このままですと解放された場所には140バイト以下の要求メモリしか対応できません。もし250バイトの要求が来たら、新しいメモリブロックを3536バイトのメモリブロックから確保する事になります。いずれ小さなメモリ要求が来たら、140バイトの空き部分が使われますが、それは分割されるかもしれず、結果としてこの領域はますます小さなフリーリストに落とし込まれてしまいます。こうなると大きなメモリ要求に答えることができなくなってしまいます。それは大変にまずいわけす。
そこで、あるブロックが解放されたら、そのブロックは自分の前後のブロックを見て、もしフリーブロックだったら「マージ(合成)」します。Boundary Tagアルゴリズムはマージも一瞬ですから、この作業は高速です。結果として、上のメモリブロックは次のようになります:
マージされて280バイトのちょっと大きなメモリブロックになりました。このマージ作業が行われたら、必ずフリーリストに再登録します。先ほど2番目の140バイトなメモリブロックが解放された時、[112-127]の範囲のフリーメモリリストに登録されていましたが、今やそれは280バイトのサイズに増えています。そのため、このメモリブロックを[112-127]のフリーメモリリストから外し、[224-255]のフリーメモリリストに登録し直します。
マージ作業には「自分の左側がフリーブロックだった場合」と「自分の右側がフリーブロックだった場合」と「両サイドがフリーブロックだった場合」の3種類があります。それぞれに対応する必要がありますが、これによりフリーブロックが隣同士に並ぶという状況が起こらなくなります(これが重要)。その結果、常に大きなフリーブロックがメモリ上に並ぶことになります。これで、確保と解放ができました。
TLSFメモリアロケータに必要な作業をちょっと整理しましょう:
確保時 ① 必要サイズを第1カテゴリーで分類
(140 -> 128-256に属する)② 第2カテゴリーで分類
(140 -> 128-159に属する)③ 第2カテゴリーに
フリーリストがあるか?ある フリーブロック決定。リストからはずす。 ない もっと大きなフリーブロックを探す(③-A) フリーブロックを分割 解放時 ① 指定アドレスのブロックをフリーに ② マージ可能な隣接ブロックがある? 無い: フリー化したブロックをリストに再登録 ある: マージしたブロックをリストに再登録
確保時及び解放時にこれらの作業をいかに高速に行えるかがTLSFの肝です。
確保① 必要サイズを第1カテゴリーで分類
ここからは実装よりのお話です。140バイトの要求があった時にそれが2のべき乗のどのカテゴリーに入るかを調べるのが最初の第1カテゴリー分類作業です。これは140をbit列で見て最上位ビットを調べればあっという間に終了するのでした。
最上位ビット(MSB)を調べる方法としては、一番上のbitから検索するというのがベタなやり方です。しかし、Visual Studioであれば組み込み関数(built-in function)の_BitScanReverse関数を使うのが便利です。これであれば一瞬でMSBを返してくれます。指定のサイズに対するMSBを返す関数を作るならこんな感じになります:
unsigned long getMSB(unsigned size) {
unsigned long index = 0;
_BitScanReverse(&index, size);
return index;
}
_BitScanReverse関数は第2引数に渡した32bitな整数の最上位ビットのインデックスを第1引数に返してくれます。論文ではこのMSBの位置の事を第1レベルインデックス(First Level Index: FLI)と呼んでいます。
確保② 第2カテゴリーで分類
140バイトが[128-256]の第1カテゴリーに分類されると出た後、続いてさらに細かい第2カテゴリーの所属先を調べます。第2カテゴリーの分割数は、ここまでの例では4分割でしたが、これはプログラマが任意に決めることができます。ただし、分割数は高速化のために2のべき乗にする必要があります。もう一つ、分割数の限度があります。例えば[4-8]カテゴリーの場合、どう頑張っても4分割しか出来ませんよね。分割数と下限カテゴリは関係があるわけです。論文では2^4=16分割もしくは2^5=32分割位が適当だよと言っています。つまり、一番小さいメモリは32バイトくらいが適当になります。この分割数のべき乗値をNとしておきましょう。例えば32分割ならばN=5(2^5)です。一番小さいメモリサイズは2^Nとなります。
先のgetMSB関数で返される140バイトの最上位ビット(MSB)は7です(8bit目)。ここから
2^7 = 128
がわかります。今分割数を4分割(N=2)とすると、下のようなカテゴリーになります:
第2段階カテゴリ(128-255) 128 ~ 159 10000000 - 10011111 0 160 ~ 191 10100000 - 10111111 1 192 ~ 223 11000000 - 11011111 2 224 ~ 255 11100000 - 11111111 3
32バイト単位で分けられています。大注目は上の赤い部分のbit列です。ここにカテゴリー番号(インデックス番号)があるではないですか!試しに8分割(N=3)した場合も見てみましょう:
第2段階カテゴリ(128-255)8分割 128 ~ 143 10000000 - 10001111 0 144 ~ 159 10010000 - 10011111 1 160 ~ 175 10100000 - 10101111 2 176 ~ 191 10110000 - 10111111 3 192 ~ 207 11000000 - 11001111 4 208 ~ 223 11010000 - 11011111 5 224 ~ 239 11100000 - 11101111 6 240 ~ 255 11110000 - 11111111 7
やっぱりMSBの下にカテゴリ番号があります。つまり、MSBと分割べき乗数Nがあると、140バイトの第2カテゴリーの所属インデックス(右の番号)は次のようなプログラムで一発で求まります:
unsigned getSecondLevelIndex(unsigned size, unsigned char MSB, unsigned char N) {
// 最上位ビット未満のビット列だけを有効にするマスク
const unsigned mask = (1 << MSB) - 1; // 1000 0000 -> 0111 1111
// 右へのシフト数を算出
const unsigned rs = MSB - N; // 7 - 3 = 4 (8分割ならN=3です)
// 引数sizeにマスクをかけて、右へシフトすればインデックスに
return (size & mask) >> rs;
}
上の関数は分かりやすくするためにマスクと右シフト数を求めていますが、もちろん一発で書いても構いません:
unsigned getSecondLevelIndex(unsigned size, unsigned char MSB, unsigned char N) {
return ((size & ((1 << MSB) - 1)) >> (MSB - N);
}
この第2レベルインデックス(Second Level Index: SLI)があれば、140バイトの所属先、そして「そこにフリーリストがあるか否か」が判定できるようになるわけです。
確保③ 第2カテゴリにフリーリストがあるか?
第2カテゴリの所属先はわかりました。そこにフリーリストがあるかどうかを判定するには非常に単純です。リストの最初のメモリブロックへのポインタがあるかどうかで判定すれば良いんです。
フリーリストのポインタ数は第1カテゴリ数×第2カテゴリの数だけあります。この2次元配列(実質1次元配列)は最初から確保してしまいます。今私達はFLIとSLIの両方を手に入れていますから、(FLI, SLI)なフリーリストにアクセスするにはFreeList[FLI * 2^N + SLI]で一発です。第2カテゴリの分割数は2^Nですから、要素数はこうなりますよね。
リストに追加されるのはBoundaryTagによって管理されているメモリブロックへのポインタです。前章のサンプルにある「BoundaryBlockクラス」がそれに該当します。このクラスは前方タグをユーザ定義できます。ここに双方向リストのためのポインタを2つ入れれば、フリーリストが簡単に作れます:
class TLSFBlockHeader : public BoundaryBlockHeader {
public:
TLSFBlockHeader *pre;
TLSFBlockHeader *next;
TLSFBlockHeader() : preBlock(), nextBlock() {}
};
// TLSF用のメモリブロックの作成例
BoundaryBlock<TLSFBlockHeader> *TLSFBlock = new(memoryPtr) BoundaryBlock<TLSFBlockHeader>(size);
詳しくは前章のサンプルをご覧頂ければと思いますが、これを前方タグとして使えばTLSF用のリンクリスト機能が付いたメモリブロックになります。
確保③-A もっと大きなフリーブロックを探す
第2カテゴリにフリーリストが無かった場合、もっと大きなブロックを探す事になります。140バイトが所属する[128-159]カテゴリにフリーリストが無かった場合、その上のカテゴリをチェックします。この時[160-191]に有るか無いか~、[192-223]にあるか無いか~といったループ検索はしません。それじゃパフォーマンスが台無しです。第1カテゴリーに所属する第2カテゴリーのフリーリストの有無をビット列で表したもの(フリーリストビット列)があるとしましょう。例えば[192-223]カテゴリ(ID=2)だけにフリーリストがある場合は、0100のようなビット列になります。140バイトはID=0に所属していますからビット列は0001です。つまり、自分のビット列よりもフリーリストビット列の値が大きければ、より大きなフリーブロックがある事になります。さらに、その中で最小なのは、自分のビット列以上の最小ビット(Least Significant Bit: LSB)です。
ちょっとごちゃっとしていますので、プログラムで示します:
unsigned char getFreeListSLI(unsigned char mySLI, unsigned freeListBit) {
// 自分のSLI以上が立っているビット列を作成 (ID = 0なら0xffffffff)
unsigned myBit = 0xffffffff << mySLI;
// myBitとfreeListBitを論理積すれば、確保可能なブロックを持つSLIが出てきます
// freeListBit = 1100 ([192-223]と[224-255]にあるとします)
unsigned enableListBit = freeListBit & myBit;
// LSBを求めれば確保可能な一番サイズの小さいフリーリストブロックの発見
if (enableListBit == 0)
return -1; // フリーリスト無し
return getLSB(enableListBit);
}
LSBを求める組み込み関数は_BitScanForward関数です:
unsigned long getLSB(unsigned size) {
unsigned long index;
_BitScanForward(&index, size);
return index;
}
getFreeListSLI関数で「フリーリスト無し」とされてしまった場合、自分が所属する第1カテゴリには確保可能なフリーブロックがありません。その場合より大きな第1カテゴリをチェックしに行きます。これもgetFreeListSLI関数の中で行ったようなビット列でのチェックができますよね。自分の所属する第1カテゴリ(FLI)よりも第1カテゴリのビット列(実質は一つの32bit整数)が大きければ、そのLSBを求める事で瞬間的に第1カテゴリIDを計算できます:
unsigned char getFreeListFLI(unsigned char myFLI, unsigned globalFLI) {
unsigned myBit = 0xffffffff << myFLI;
unsigned enableFLIBit = globalFLI & myBit;
if (enableFLIBit == 0)
return -1; // メモリが完全に無い!!
return getLSB(enableFLIBit);
}
つまり、フリーリストの有無を検索するのは上記のビット演算を数回繰り返すだけなんです。これはループ検索よりももちろんはるかに高速です。
解放① 指定アドレスのブロックをフリーに
ここからは解放のお話。解放する時にはTLSFメモリアロケータが渡した生アドレスが指定されてきます。前章のサンプルにあるBoundaryBlockクラスはそのアドレスから自分の位置を割り出せます。理由は簡単で、アドレス位置のsizeof(BoundaryBlock)前に自分自身が存在している事が保障されているためです:
外に渡すのは緑色部分の先頭アドレスで、前方タグサイズはsizeof(BoundaryBlock)です。
ブロックをフリーにするのは前方タグ内にある使用中フラグを下ろすだけです。
解放② マージ可能な隣接ブロックがある?
解放したブロックは、そのままだとどんどん細分化されてしまいますので、となりのブロックがフリーブロックであればそれをマージする必要があります。この作業はメモリブロックがBoundary Tagアルゴリズムであれば非常に簡単です。前章のサンプルにあるBoundaryBlockクラスにはすでにその機能をつけてあります。自分の隣が使用中かフリーかはフラグを見れば一発ですし、マージもあっという間にできます。
マージされたフリーリストは外される必要がありますが、これはブロックが自分自身でできてしまいます。マージ後に確保されたより大きなメモリブロックはフリーブロックとして再度登録される事になります。
これがTLSFメモリアロケータのアルゴリズムのほぼすべてです。プログラム上での細かい調整は少しありますが、このアルゴリズムによってフラグメンテーションが少なくて高速検索されるメモリアロケータになります。論文中でもパフォーマンス比較が行われており、手に入っている2008年くらいまでのメモリアロケータの中では最強に近い物のようです。フラグメンテーションが少ないのは、第2カテゴリで使用可能なメモリサイズが細かく分類されている事が大きいです。論文ではこれにより最大でも25%程度しかフラグメンテーションが起こらないという結果が出ています。
実装はなかなかに大変ですが超魅力的ですね(^-^)