ホーム < ゲームつくろー! < DirectX技術編 < キーフレームアニメーションで動きを制御
その8 キーフレームアニメーションで動きを制御
ゲームは1秒で60コマもあります。ですから、1つ1つのオブジェクトの動きをコマ単位で定義していてはキリがありません。しかし、「現在の位置から次の位置まで4秒で直線移動」となると、途中の240コマは計算で補間する事が出来ます。このように動きの節となる部分を設定して、途中の補間位置は計算で求めるオブジェクトの動かし方を「キーフレームアニメーション」と言います。
キーフレームの考え方は、何もオブジェクトの位置のみに留まりません。例えば、カメラの動き、回転、ライトの光量、さらにはオブジェクトの色や透明度の変化などもすべてキーフレームの考え方が適用できます。こういうのはクラス化してしまうと強力な武器になります。具体的な実装は「DirectX クラス構築編」で述べる事にしまして、ここではキーフレームの計算方法に焦点を絞りたいと思います。
キーフレームの単位となるのは基本的には「時間」です。同じ2点間の移動でも、時間が異なれば、1コマ当たりの移動量も変わってきます。その事に注意しながら考えていきましょう。
① 線形キーフレーム
おおよそ殆どの動きは点と点を結ぶ線で表現できます。例えば原点からx=1の位置まで10秒で進むとするなら、1秒後にはx=0.1の所にいます。計算も単純で実装もしやすいのが線形キーフレームです。
線形キーフレームは現在の値、次の節までの値、そしてフレーム間の時間があれば補間位置を決める事が出来ます。ここではまず最も単純な設定をします。現在の値をc(current)、次の節での値をn(next)、フレーム間の時間をt(time)としましょう。この時、現在からfフレーム後の値lv(f)は、
lv(f) = c + f * (n - c)/t
となります。fは0~tの間の自然数です。
この最小限のキーフレーム計算があれば、直ぐに3次元座標の線形キーフレームに拡張できます。現在の位置を(cx,cy,cz)、次の節での位置を(nx,ny,nz)、フレーム間の時間をtとすると、fフレーム後の補間位置は,
(lvx(f),lvy(f),lvz(f))
となります。lv(f)を最小のクラスとしておいて、座標の線形キーフレームはそのコンポーネントを持つようにすれば、直ぐに実現できそうです。
実は、Direct3DXのヘルパー関数であるD3DVec3Lerp関数を使うとこの線形補間座標を簡単に計算してくれます。
D3DXVECTOR3 *D3DXLerp( D3DXVECTOR3* pOut, CONST D3DXVECTOR3* pV1, CONST D3DXVECTOR3* pV2, FLOAT s )
pOutに線形補間点の座標が返ります。
pV1には始点の座標が入ったD3DXVECTOR3構造体へのポインタを渡します。
pV2は終点の座標です。
sは補間比率です。s=0ならば始点、s=1ならば終点が入り、s=0.5ならば2点間の中点の座標となります。
他の座標表現をしたい時も良くあります。例えば、XY平面上のどこか1点を中心にオブジェクトをぐるぐる回したい事などがあります。そういう時は直交座標よりも極座標の方が設定が簡単です。極座標は半径rと回転角度wで点を示す方法です。これも同様に線形キーフレームが使え、次のようになります。
(r, lvw(f))
ここで、
lvx(f) = r * cos(lvw(f))
lvy(f) = r * sin(lvw(f))
という関係があります。半径rにも線形キーフレームを適用すると、渦巻き軌道を描くようになります(これはアルキメデスの螺旋と呼ばれる軌道です)。
② HermiteSprine曲線キーフレーム
線形キーフレームは次の節に進む時に軌道が折れてしまいます。やはり複数の点が並んでいる時に、それをスムーズ結んで行きたいと思うのが心情です。そういう時にはよくスプラインという補間法が使われます。ただ、スプラインはちょっと扱いが面倒なんです。ここで紹介するエルミートスプライン曲線は「通過点」と「制御バー」を用いてスムーズに点を結んでいく方法で、スプラインよりも高い自由度を持ちます。まずは、下の図をご覧下さい。
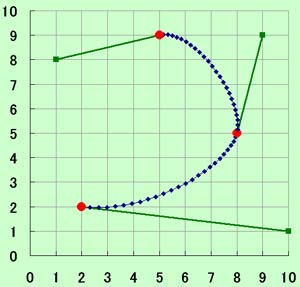
Excelで綺麗に書くのは工夫がいりますね
赤い点が「通過点」で、緑の線が「制御バー」です。これだけで、3点がスムーズに結ばれています(数学的に連続)。これを実現したいわけです。しかし、どう計算してよいやらわかりませんよね。
まず結論から言ってしまいます。Direct3DXのヘルパー関数であるD3DXVec3Hermite関数を用いると、上の点を簡単に算出してくれます。
HRESULT D3DXVec3Hermite( D3DXVECTOR3 *pOut, CONST D3DXVECTOR3 *pV1, CONST D3DXVECTOR3 *pT1, CONST D3DXVECTOR3 *pV2, CONST D3DXVECTOR3 *pT2, FLOAT s );
pOutに2点間の補完点が返されます。これはD3DXVECTOR3構造体なので3次元ベクトルとして返ります。つまり、上の図では2次元でしか示していませんが、この関数は「3次元のエルミートスプライン曲線」の補間点を計算してくれる優れものなんです。
pV1には始発点の座標を与えます。
pT1にはpV1から伸びる制御バー(上図の緑のバー)の大きさをベクトルで与えます。例えば、上の左下の赤点を始点とすると、制御バーは大きさなので(8,
-1,0)となります。
pV2は終点の座標を与えます。
pT2にはpV2の制御バーの大きさを与えます。
sは補間位置を0~1の間で与えます。s=0ならば始点、s=1ならば終点がpOutに返ります。その間であれば比率に見合った点が計算されます。これがキーフレームとして使えるわけです。
内部でどういう計算が行われているかは目をつぶり、これをツールとして使ってしまいましょう。
エルミートスプライン曲線は各点の制御バーを与えるのが少し面倒かもしれません。もし、ある程度適当でも良いのであれば、1番最初の制御バーの大きさとそれぞれの点の位置関係から自動計算させてしまうのも手です。
例えば、始点P1と1つ飛ばした点P3までのベクトルをV1、そして始点の制御バーの大きさのベクトルT1を足し算して次の制御バーの大きさT2としてしまうのです。T2を成分で表すと、
T2.x = P1.x - P3.x + T1.x
T2.y = P1.y - P3.y + T1.y
T2.z = P1.z - P3.z + T1.z
となります。
上の図がその模式図で、P1の制御バーのベクトルとP3の合成ベクトルをP2の制御バーのベクトルにしています。簡単な計算なのですが、そこそこの結果が期待できます。この方法で最初に示したグラフと同じ点に対して描画したのがこちらです。
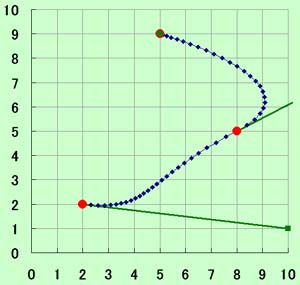
これでも十分にいけます。ちなみに、最後の点の制御バーには大きさがありません。
各点と最初の点の制御バーの大きさを与えるだけで曲線が描けるので、とても使い勝手が良くなります。
後はフレーム間毎の区分率sを計算するだけで、①の線形キーフレームがそのまま使えます。すなわち、lvs(f)を算出すればOKです。
③ 複数点間等速運動
①の線形キーフレームにせよ、②のエルミートスプラインにせよ、節ごとに移動距離を決めるので、当然その移動速度は節で異なってしまいます。時には、キーとなる座標を複数決めて、その間を同じ速度で進んでもらいたいと思う事があります。
「10個先の点まで120フレームで行ってほしい」と考えた時には、1ステップで進む距離を計算する必要があります。そのためには、10個先までのトータル距離が必要です。
線形キーフレームの場合トータル距離Dを求めるのは簡単です。2点間の距離を合計すればよいのですから、座標P1(x1,y1,z1)、P2(x2,y2,z2)について、
D = sqrt( (x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2 )
と計算します。Direct3DXのヘルパー関数にはD3DXVec3Length関数というベクトルの長さを計算してくれる関数がちゃんとあります。
FLOAT D3DXVec3Length( CONST D3DXVECTOR3* pV );
pVが長さを求めたいベクトルです。
2点間の場合は、そのベクトルを求めるために座標の引き算をする必要があります。これは、D3DXVec3Subtract関数を用います。
D3DXVECTOR3* D3DXVec3Subtract( D3DXVECTOR3* pOut, CONST D3DXVECTOR3* pV1, CONST D3DXVECTOR3* pV2, );
pOutにはpV1-pV2の結果が返ります。また戻り値にも同様の値が返りますので、長さを一気に求めたいのであれば、
D = D3DXVec3Length(D3DXVec3Suvtract(pOut, pV1, pV2));
とすれば求まります。最初にあげた成分に分解した式とDirectXが用意した関数を利用したこの式と、どちらでも使いやすい方を選択すれば良いでしょうね。
複数点間の長さと必要ステップ数がわかれば、1ステップでの移動距離がわかります。今は補間点を求めたいのですから、始点から1ステップずつ直線移動をしていって、その座標を求めればよい事になります。ただし、1ステップの間に節をまたぐ事があります。その場合、幾つの節をまたいだかを算出して、最新区間の正しい位置を計算しなければなりません。下の図をご覧下さい。
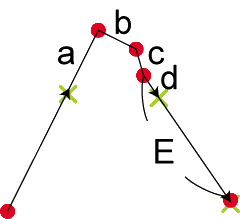
図で左の「×」の次が右の「×」になるのですが、その間に3つの節をまたいでいます。1ステップでの移動距離をEとすると、d=E-(a+b+c)です。4番目の点(P4)からdだけ進んだ位置というのは、P4~P5の区間のd/E分になるので、右の×の位置は、
P×=P4 + d/E * (P5 - P4)
となります。これをうまく自動計算する関数を作ってしまえば、線形キーフレームによる複数点間等速移動が実現できます。
エルミートスプラインで等速運動をさせたい場合、本当ならば線形キーフレームの時と同様に曲線の長さを求めてそれをフレーム数で分割したいのです。しかし、エルミートスプライン曲線の長さを解析的に求める事は無理です。そこで、上の方法がさっそく応用できます。エルミートスプラインの適当な補間位置を求めておいて、それを線形キーフレームで近似します。次に上の方法で移動位置を求めれば、曲線的な動きに近くなります。ゲームとして扱う分にはこれで十分です。
速度に重点を置くならば、線形キーフレームがダントツ速いです。複数点間の等速運動も異常な点の数を扱わなければ、計算はほぼ一瞬でしょう。エルミートスプライン曲線も裏では単なる3次関数の計算をしているだけなのでかなりに高速です。60フレームのゲームで通常の使用であれば、これらはまったく問題なく動作するでしょう。ただ、例えば弾幕系STGの溢れんばかりの弾にエルミートスプライン曲線を使ったりするのは止めた方がいいです。これはさすがに荷が重い計算になります。自機の武器などの使用には十分可能でしょう。ただ、ホーミングなどはもっと別の軽い実装方法があります。
カメラワークはキーフレームによって随分と楽になります。特にDirectX Graphicsの視点変換(ビュー変換)は「注視点」という見つめる点を定義してカメラの方向を決めるので、キーフレームでカメラを動かしながら、オブジェクトをとり続けるなどというワクワクする使い方が出来るようになります。
クラス化については、ここでもう殆ど中身を説明してしまったかもしれません。通過点の座標と制御バーの大きさを定義した点クラスを作り、そのクラスを配列で扱うキーフレームクラスを作成すればいいだけです。簡単で応用範囲の広いクラスが出来ると思います。これについては「DirectX クラス構築編」で検討します。