ホーム < ゲームつくろー! < DirectX技術編 < でこぼこの床ををまっすぐ走らせるには?
その29 でこぼこの床をまっすぐ走らせるには?
RPGの大地やオフロードレースのコースは、通常でこぼこしています。同じでこぼこ床ではありますが、両者には決定的な違いがあります。RPGのキャラクタは、きっと大地が多少傾いていたとしても、重力に対してまっすぐ立つでしょう。それは人が坂道を登っても空を上にする点からも矛盾の無い考えです。それに対してオフロードレースの車は、傾きに対して垂直な姿勢をとるはずです。空を上にするか、平面の法線を上にするか。両者はここで違うわけです。この両者が、でこぼこ床に沿ってある方向に進みたいとします。その時、次に進むべき位置と姿勢をどう定めればよいのでしょうか?
この章では、でこぼこした床をまっすぐ走らせるための位置決めと姿勢制御について考えてみることにします。
① 問題は位置よりも進みたい方向
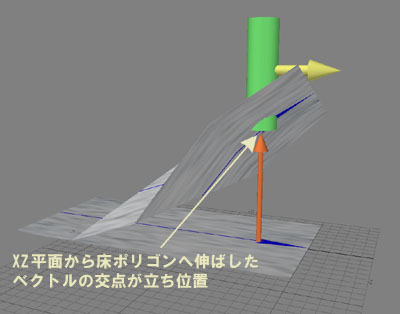
重力方向にまっすぐ立つことを前提としたRPGのキャラクタの場合、地面に立たせることはとても簡単です。言葉で言うと「床ポリゴンに対するY軸と反対方向への射影点」が立ち位置です。これを図で示すとこうなります。
Y軸方向が上方向とするゲームでは、キャラクタの位置は通常XZ平面で表されます。Y座標は、XZ平面から床ポリゴンへ伸ばした直線との交点になります。これについては衝突判定編3D衝突編その8「床ポリゴンの高さを知るには?」で同じ事を示しておりますので、ここでは説明を割愛します。
問題は位置ではなくて「方向」です。この章のメインはその説明になります。
ローカル座標にあるキャラクタをワールド座標にてまっすぐ走らせるには、少なくともワールド空間における「行こうとする方向」を定める必要があります。これは、前の進行方向からの差分で考えるのが普通です(いきなりワールド空間の方向を決めるのは無理)。ただワールドを知らないローカルオブジェクトにとって、上下の差分は大抵決められません。できることと言えば、自分が今立っている平面に対して前後左右どちらに行くかという「2Dの方向差分」しか決められないんです(プレイヤーがコントロールするキャラクタならなおさらです)。その場合、床はでこぼこしていますから、そのまま進むと土にめり込んでしまうか、空を飛んでしまいます。次に進みたい方向は、あくまでも「行きたい方向の指針」のようなものなんです。ちょっと数学っぽくいうなら「瞬間方向」もしくは「接ベクトル」とでも言うのでしょうか。
話が野暮ったくなっちゃいましたが、用は瞬間的に行きたいという方向がまずあるということです。図を見てみましょう。今、下図のように、ある位置から次の位置へ進みたいと考えます。
次に行きたい瞬間方向が、XZ平面に沿った青い矢印で表されています(今立っている平面に含まれるベクトルです)。ローカル座標にあるキャラクタはまだ次の向きを向いていませんから、上図のように次の位置に言っても、向きがおかしくなっています。これを正しくするには、ローカル座標にあるキャラクタをY軸を中心に回転させなければなりません。その回転角度は、上の図を真上から見ればばっちりわかります。
今の位置から次に進みたい方向ベクトルを定めた時、キャラクタが向くべき角度は、その進行方向ベクトルとキャラクタの正面(普通Z軸方向)との内積で計算ができます。後は、算出した角度を用いてY軸中心にキャラクタを回転させれば、次の位置でも正しい方を向きます。
Y軸方向が空であり、常に空方向に頭を向ければよい場合、床のでこぼこはキャラクタの向きに影響を及ぼさないので、平坦な地面を歩かせるのと実質変わりません。大変楽に姿勢制御ができるわけです。
② 平面に吸い付くキャラクタをまっすぐ走らせる
さて次は、レーシングゲームなどで平面に吸い付く機体をまっすぐ走らせる事を考えます。まずはその状況を図にしてみます。
平面上の一点に位置することは先ほどと一緒です。先ほどと違うのは、キャラクタが平面に対して垂直に立ち、「でこぼこ床に投影された青矢印の方向」に向いていることです。これは「グローバルな空方向という概念が無い」状況です。ちょっとやっかいですが、少しずつ噛み砕いて説明していきましょう。
まず、次回に行きたい方向がすでにあるとします。
上図は床ポリゴンを省いてあります。この行きたい方向はあくまでも、「キャラクタが立っている平面と平行」です。空方向が無いので、上図のようにXZ平面に平行でなければならない理由は全くありませんのでご注意下さい。
ここに床ポリゴンを付け加えて、キャラクタの次の立ち位置を決定します。
現在のキャラクタが立つ平面から行きたい方向をまっすぐ伸ばし(水色の矢印)、その平面の法線(オレンジの矢印)を床ポリゴンに伸ばします。この交点が次にキャラクタが移動する位置です。これで立ち位置はわかりました。
交点を含む平面に垂直に立つには、ローカル座標にあるキャラクタの上方向(Y軸)を、平面の法線方向に傾ければ良いだけです。
この回転軸は「ローカル座標のキャラクタの上方向(Y軸)と平面の法線(赤い矢印)に垂直です。これは、外積で求められます。この回転方法については、DirectX技術編その16「オブジェクトを任意の平面に立たせる姿勢制御」で説明した方法と全く一緒なので、イメージが沸かない方はそちらも合わせてご覧下さい。
この1回目の回転(姿勢合わせ回転)の後、方向あわせ回転をします。ここが今回の最大の肝です。
キャラクタはすでに平面に立っていますので、後は赤いベクトルで示した平面の法線ベクトルを軸としてキャラクタを回転させれば良いのですが、問題はその回転角度です。これを求めるには、最初に示した「キャラクタが次に行きたい方向のベクトル(水色の矢印)」そして「最初に立っていた平面の法線ベクトル(オレンジの矢印)」を利用します。
キャラクタが次に向くべき方向の指針は水色のベクトルで、最初に立っていた平面の法線ベクトルはオレンジ色の矢印で示されています(こちらを向いています)。上図のように、赤色の法線ベクトル(移動後の平面の法線)を軸にして、黄色いベクトルが「水色とオレンジのベクトルによってできる平面」に平行になるように回すと、行きたい方向を向きます。平面に平行であるというのは、「平面の法線と垂直である」と意味は同じです。上図の紫のベクトルは水色とオレンジのベクトルの法線で、先ほどの話から、黄色のベクトルと垂直関係にあります。
回転前の矢印(ワイヤーフレームで表されています)と紫のベクトルとの内積によって計算される角度をRとしましょう。上の図だとR=130度くらいでしょうか。このRを90度にすれば良いのですから、単純な引き算で40度だけ逆回転(時計回りが順回転なので)させれば良い事がわかります。少し一般化すれば、ワイヤーフレームの矢印を黄色の矢印まで回転させるための回転角度R2は、90度(=π/2)からRを引き算した値になります。
もうちょっと記号を使ってまとめます。方向合わせに必要な回転角度R2は、進みたい方向と、立っていた平面の法線ベクトルに垂直であるベクトルV(紫)と、姿勢合わせの後のキャラクタの前方向ベクトルD(ワイヤーフレームの矢印)との内積Rから、
R2 = π/2 - R = π/2 - ACOS(V・D/(|V|・|D|))
で算出されます。Dさえ求められれば、もう何も考えずに回転角度を算出できますね。
さて、この作業でめでたく移動ができました。移動した段階で、立っている平面の法線(オレンジ色のベクトル)がまず更新されます。次に進みたい方向(水色のベクトル)は、黄色のベクトルの方向を差分角度(ローカル座標のキャラクタがY軸を回転軸として新規に回転した差分角度)だけ軸回転させることで得られます。ここにも区オータニオンがありますね。オレンジと水色のベクトルがあれば、同様にして次のポジションを決めていくことができます。これによって実質「平面の壁」だって登れるキャラクタになります。
②の方法は、平面が連続的に多少なだらかに繋がっている状況で利用できますが、コークスクリューのように、平面が激しくねじれる場合だとうまく行かない可能性があります。その場合、いっぺんに次の到達地点まで進めるのではなくて、少しずつ進めなければならないかもしれません。計算量は増えてしまいますが、致し方ないところでしょう。
まっすぐ進めるための方法を色々と説明してきました。②のレベルまでやる必要があるかは、作成するゲーム次第なので、わざわざ難しいことをする必要があるかどうかを最初に考えるべきでしょうね。大抵は①で説明した地面があるゲームですから楽できるはずです。しかし、②のゲームだってやっぱりあるわけでして、おろそかにはできない姿勢制御かなと思います。
③ 謝辞
この記事を書くきっかけを与えて下さいましたhis様に感謝申し上げます。