ホーム < ゲームつくろー! < DirectX技術編 < 深度バッファシャドウの根っこ:影を描画してみる
その46 深度バッファシャドウの根っこ:影を描画してみる
深度バッファシャドウの実現に向けて、ここまで基本理論(その44)、Z値テクスチャの作成(その43、その45)と繋げてきました。概要はこれでばっちりです。この章ではいよいよ深度バッファシャドウのレンダリングに向けて話を詰めて行きたいと思います。とは言ってもここからもまた細かく長く大変だったりするのですが、少しずつ掘り下げていきますので大丈夫です。ただその43と44の理解が前提となりますので、まだと言う方は一度そちらを確認してみてください。
① ライト目線のZ値テクスチャを作成した後の話
ライトの方向からみたオブジェクト群のZ値テクスチャを作成(その43)した後、深度バッファシャドウを描画するための2回目のレンダリングに入ります。このレンダリングでは「カメラから見た通常シーンの描画」が行われます。しかし、描画する時にスクリーンに打つ点の色を「影」か「明」か判断します。この判断をどう行うか、その基本原理はその44で述べましたが、ライト方向からのZ値をレンダリング時にもう一度計算(以下それを再計算Z値と呼びます)して、すでに計算してあるライト方向からの本当のZ値(リアルZ値と呼んでおきます)と比較します。再計算Z値がリアルZ値よりも大きい(奥にある)場合、ライトの光が届かないので、その点は影であると判断できます。
打つ点の色をレンダリング開始後に判断できるのは「ピクセルシェーダ」だけです。しかし、再計算Z値を計算するには、その43で説明したような頂点シェーダでの仕込みも必要になります。シェーダプログラムについてまだちょっとと言う方は、プログラマブルシェーダ編のHLSL部分をご覧頂下さい。私もその程度の知識でこの章を書いております(^-^;。
② 頂点シェーダにある2つのルート
先に申しましたように、2回目のレンダリングの目的はあくまでもカメラからみたシーンを描画することにあります。ですから、オブジェクトを描画して最初に飛び込んでくる頂点シェーダには通常の描画ルートがちゃんとあります。すなわち、ローカル座標にある頂点をワールド空間に置いて、カメラのビュー、射影空間に変換するすっかりおなじみの作業です。
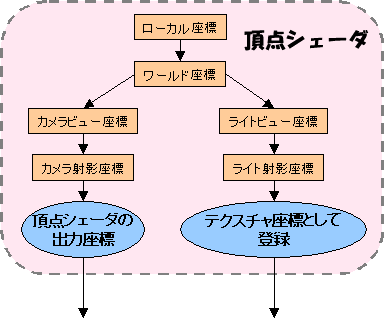
ただもう一方で、同じ頂点を「ライトの目線から見た時のZ値(再計算Z値)」を算出する仕込みがここに入ってきます。この流れ自体はZ値を算出する原理を述べたその43に詳しく説明してあります。つまり深度バッファシャドウのレンダリングでの頂点シェーダには、1つの頂点に対するカメラ側の変換とライト側の変換という2つの流れが同時に存在するわけです:
左側の流れが本流、右側が明暗判定用の流れです。本流はレンダリングされる頂点なので、頂点シェーダの出力、明暗判定用の流れは再計算Z値を算出するのでテクスチャ座標に登録します。
③ 頂点シェーダの実装
深度バッファシャドウの頂点シェーダのメインは、上のルートにあるように頂点を変換するだけです。そのために、ワールド座標変換以降の上に示5つの行列を定義します:
深度バッファシャドウの頂点シェーダ float4x4 matWorld : world; // ワールド変換行列
float4x4 matCameraView : view; // カメラビュー変換行列
float4x4 matCameraProj : projection; // 射影変換行列
float4x4 matLightView; // ライトビュー変換行列
float4x4 matLightProj; // 射影変換行列
struct VS_OUTPUT
{
float4 Pos : POSITION; // 射影変換座標
float4 ZCalcTex : TEXCOORD0; // Z値算出用テクスチャ
float4 Col : COLOR0; // ディフューズ色
};
// 頂点シェーダ
VS_OUTPUT DepthBufShadow_VS( float4 Pos : POSITION , float3 Norm : NORMAL)
{
VS_OUTPUT Out = (VS_OUTPUT)0;
// 普通にカメラの目線によるワールドビュー射影変換をする
float4x4 mat;
mat = mul( matWorld, matCameraView );
mat = mul( mat, matCameraProj );
Out.Pos = mul( Pos, mat );
// ライトの目線によるワールドビュー射影変換をする
mat = mul( matWorld, matLightView );
mat = mul( mat, matLightProj );
Out.ZCalcTex = mul( Pos, mat );
// 法線とライトの方向から頂点の色を決定
// 濃くなりすぎないように調節しています
float3 N = normalize( mul(Norm, matWorld) );
float3 LightDirect = normalize( float3(matLightView._13, matLightView._23,matLightView._33) );
Out.Col = float4(0.0,0.6,1.0,1.0) * (0.3 + dot(N, -LightDirect)*(1-0.3f));
return Out;
}
シェーダの中身はカメラの目線による頂点変換と、ライトの目線による変換をそれぞれ独立に行っています。カメラ目線の変換後頂点はシェーダの出力頂点に、ライト側はVS_OUTPUT.ZCalcTexテクスチャ座標として出力させています。頂点のディフューズ色は、法線とライトが向いている方向からディフューズ色の基本式で算出するにとどめました。ここでは描画色を固定していますが、本来はちゃんと頂点色を使う必要があります(簡潔のために今はこうしました)。
このプログラム自体に難しい部分は何もありません。3Dゲームの基本であるワールド変換、ビュー変換そして射影変換を用いて頂点を変換しているだけです。このプログラムを通った頂点とテクスチャ座標は、次にピクセルシェーダに渡されます。
③ ライト目線の出力を「テクスチャ座標」にするんです
ピクセルシェーダですべき事をもう一度ご覧下さい:
ピクセルシェーダには2つの情報が入ってきます。1つはカメラの目線で見た時のポリゴン表面のピクセル色(ラスタ化されたもの)、もう1つはライトの目線で見た時の「射影空間座標にあるピクセルの座標」です。この座標点から再計算Z値が算出されます。そして同じアングルで先に計算された「リアルZ値」と比較することで、ピクセル色の明暗判断ができることになるわけです。
ここで問題となるのは「射影空間にある座標に該当するテクスチャの座標」です。スクリーンに射影された点も、それがテクスチャのどの点に該当するかわからないとまったく使えませんよね。ですから、そこには明確な射影空間→テクスチャ空間の変換が必要になります。ちなみに、この変換はどえらく簡単である事を先に告げておきますね。
以下は変換の理屈の説明ですから「知ってるよ」という方は飛ばして構いません。まず、先に作成している同じライト目線で作成したZ値テクスチャを座標付きで示します:
テクスチャ座標は左上を原点として、右方向をX、そして下方向をYとします。そして通常テクスチャは0~1の間に正方形で定義されます。
一方ライト目線で見た「射影空間座標」として入ってきた点に注目してみます。射影変換後の段階で、頂点は次のような座標に変換されています:
射影座標は右方向をX軸、そして上方向をY軸とし、ライト目線のカメラが捕らえた範囲にある頂点は-wから+wの間に収められます。この「w」というのは実は頂点(x,y,z,w)の4つ目のw成分値です。面白い事に、射影変換をすると自分が持つwの範囲にすっぽり収められてしまうんです。興味のある方は射影変換行列に視錐台の境界線上にある点を掛け算してみると範囲が確認できますよ。
目標は上の座標にある絵をテクスチャ座標に持っていく事です。そこで以下に示す何枚かの図でその変換を体感してみましょう。まず、上の正方形内の頂点を全部wで割ってしまいます。すると、次のようになります:
wは全部1に標準化されます。次にテクスチャと軸の向きを合わせてみます。これは、Y軸をひっくり返すだけです:
軸の方向がテクスチャ座標と合いました。この作業自体は物の見方を変えただけなので、足し引き等は何もしていません。ひっくり返すと描かれている絵が上下逆さまである事がわかります。でも左右はそのままです。そこで、次は緑色の頂点のY座標の符号を逆にしてみます:
X軸を挟んで絵を対称移動させることになるので、Z値テクスチャと軸の方向も絵の向きも合いました。続いて左上が原点に来るようにこの絵を右下方向に平行移動します:
もう何か見えてきました(^-^)。最後は、絵のスケールを全部半分にすると、めでたくZ値テクスチャとぴったり同じになります。
ここまで行った変換工程をもう一度まとめます。まず射影変換された頂点を自身のw成分で割り算して標準化しました。次はy成分を反転しました。これは符号を逆にする事で、すなわちy成分にマイナスを付ければそうなります。その次にxy成分それぞれに1を足し算して、正方形の左上を原点に平行移動させました。最後にスケールを半分にしました。これだけです。これを式でそのまま書くと次のようになります:
点をwで割って、Yはマイナスにして1足して2で割る。これが射影変換した頂点をテクスチャの座標に変換する式なんです。これをピクセルシェーダに実装します。
④ ピクセルシェーダの実装
理屈がわかれば、ピクセルシェーダの実装は簡単です:
深度バッファシャドウのピクセルシェーダ // ピクセルシェーダ
float4 DepthBufShadow_PS( float4 Col : COLOR, float4 ZCalcTex : TEXCOORD0 ) : COLOR
{
// ライト目線によるZ値の再算出
float ZValue = ZCalcTex.z / ZCalcTex.w;
// 射影空間のXY座標をテクスチャ座標に変換
float2 TransTexCoord;
TransTexCoord.x = (1.0f + ZCalcTex.x/ZCalcTex.w)*0.5f;
TransTexCoord.y = (1.0f - ZCalcTex.y/ZCalcTex.w)*0.5f;
// リアルZ値抽出
float SM_Z = tex2D( DefSampler, TransTexCoord ).x;
// 算出点がシャドウマップのZ値よりも大きければ影と判断
if( ZValue > SM_Z+0.005f ){
Col.rgb = Col.rgb * 0.5f;
}
return Col;
}
最初にライト目線での最計算Z値を算出します。次に射影空間にあるその点のXY座標をテクスチャ座標に変換します。これは③でくどいほど説明して導いた式を使います。ここで求めたテクスチャ座標に該当するリアルZ値をテクスチャから抽出します。再計算Z値(ZValue)とリアルZ値(SM_Z)を比較し、再計算Z値が奥にある、つまりSM_Zよりも値が大きい場合はその点に光が届かないので、その点は影であると判断されます。影だった場合、引数のColに入ってきた点の色濃度を等しく半分に暗くしています。
これで、深度バッファシャドウの実装はほぼ終了です。後は、プログラム側で「Z値テクスチャ作成」と「深度バッファシャドウによるレンダリング」を通して行えば、ちゃんと影が生成されます!この完全サンプルプログラムはこちらで公開致しますので、どうぞ一度お試し下さい(実行形式もあります)。
⑤ 深度バッファシャドウの天敵「マッハバンド」
ところで、上のピクセルシェーダ内に強調した「0.005f」。これみよがしに赤くしてみました(^-^;。「なんで0.005fをZ値テクスチャの値に足しているの?」と思われるかもしれません。
0.005fを足していない場合と足した場合とで、レンダリング結果をご覧頂下さい。これは、本章のサンプルプログラムでテストしました:
左が足していない場合、右が足した場合のレンダリング結果です。双方とも地面に影が落ちていて万々歳なんですが、左側はすごい縞々ですよね。ブラインド越しの影のようです。これは「マッハバンド(Mach Band)」と呼ばれる深度バッファシャドウの天敵となる現象が露骨に出ているんです。右側は0.005fを足し算しただけですが、マッハバンドが消えています。どうしてこんな事になるのか、理由を探ってみます。
深度バッファシャドウを実現するには、最初にZ値テクスチャを作成します。これはライト方向から見たZ値を色情報としてテクスチャに格納します。本来のZ値は0~1の「浮動小数点値」です。しかしテクスチャは、例えば256段階の整数(のようなもの)に浮動小数点を丸めしまします。これが悪さを引き起こしているんです。
以下は考えやすいようにZ値を255倍して8bitの色情報と同スケールにして説明しています。あるピクセルのZ値が175.3だとしましょう。テクスチャは整数ですからこの小数点を直接格納できないため、Z値を何らかの近似値に丸めます。これはビデオカードによるかもしれませんが、大抵は四捨五入されて「175」という値になります。そのすぐ近くのZ値が175.6くらいだったとします。すると、今度は176に丸めます。さて、その結果滑らかだったポリゴンがどうなるか、下図をご覧下さい:
これはポリゴン面を真横から見ている状態です。右側からポリゴン表面にライトが当たっているとしますと、本来滑らかなポリゴン表面のZ値は、テクスチャに登録された時点で整数値単位にガタガタにされてしまいます。
ここで明暗判定のため同じポリゴン表面のライト側から見たZ値もう一度計算すると、ガタガタのポリゴンと滑らかなポリゴンのZ値を比較をすることになります。すると、次のようなマッハバンドが出現するんです:
先に示したレンダリング結果がブラインド越しの影のように綺麗なスプライトになるのはこのためです。
そこで、ガタガタになったポリゴンのZ値をあえて1だけ大きくしてみます(上の図では左へずらす)。すると、
従来の滑らかなポリゴンはガタガタのポリゴンよりも常にライト側に近いと判断されるため、マッハバンドは綺麗に消えます。今Z値は255倍しているので、理屈では1/255=0.004程度ずらすと確実なんですが、大事を取って0.005fをZ値テクスチャの値に足しているというわけです。
「じゃぁ、これでマッハバンドはもう気にしなくていいんだね」と思われるかもしれません。しかし、この子は実は至る所に出現します。特に影と明の境目で非常に顕著に現れます。0.005fを足した時の別のレンダリング結果をご覧下さい:
ギザギザのマッハバンドがやはり出現しています。これは影になる部分と明るい部分との境目でfloat型の浮動小数点が暴れるために起こります。このタイプのマッハバンドは離散的なPCの世界では少なからず起こります。ただし、Z値の解像度が大きくなると前後関係が明確になるために、このマッハバンドの見え方はぐっと小さくなります。Z値テクスチャの解像度の向上がマッハバンド削減のキーなんです。このために現在標準化されつつある仕様が「浮動小数点テクスチャ」です。丸め誤差をなくす事でバンドの発生を減らそうと試みられています(そでも離散である事には変わりないので、出るものは出るんですが・・・)。
なんだか図だらけの章になってしまいました。重くて申し訳ありません。これで、深度バッファシャドウの描画までとりあえず辿り着けました。後はこれを色々なポリゴンオブジェクトに対して対応させていく作業になっていきます。通常の簡単なプリミティブや固定頂点メッシュであればこれで十分です。ところが、、スキンメッシュに対応するとなると、急に大変になります。というのは、固定機能パイプラインが裏で自動的に行ってくれていた「1つの頂点への重み計算」を自前でやる必要が出てくるためです。もちろん頂点シェーダの中でです。よって、いきなりスキンメッシュに進むのはちょっと無理があります。
そこで、プログラマブルシェーダ編でスキンメッシュが可能な頂点シェーダの作成方法について試行錯誤し、一方でアニメーション可能なクラスをちゃんとまとめてから、改めて深度バッファシャドウをそこに適用してみたいと思います。道は長いのですが、そこまでできてようやくプロフェッショナルな世界の玄関前の引き戸に手をかけるという感じでしょうね。プロはホントに凄いもんです(^-^;