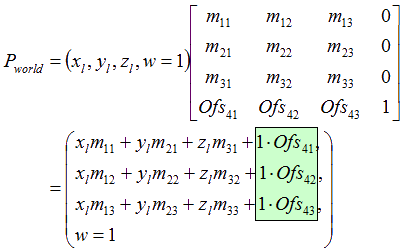
儂乕儉 < 僎乕儉偮偔傠乕両 < DirectX媄弍曇
偦偺55 偦傕偦傕乽w乿偭偰壗側偺偐丠
丂儘乕僇儖嵗昗偵偁傞捀揰偼(x,y,z,w)偲偄偆4師尦偺儀僋僩儖偱掕媊偝傟傑偡丅乽w乿ゥ眰陙A撲側懚嵼偱偡丅偟偐傕丄儘乕僇儖嵗昗偵偁傞忬懺偱偼丄w=1偲偟傑偡丅w=1ゥ葌簛H偳偆偟偰0偠傖側偄偺丠偦傕偦傕僐儗壗丠壗偵巊傢傟偰偄傞偺丠偳偆偟偰昁梫側偺丠撲側懚嵼偺媈栤偼恠偒傑偣傫丅
丂偦偙偱丄偙偺復偱偼偦傫側晄巚媍側懚嵼w偺抣偺堄媊偵偮偄偰挷傋偰傒偨偄偲巚偄傑偡丅
嘆 w偺曄壔偺椃傪尒偰傒傛偆
丂w偑幚嵺偵偳偆嶌梡偟偰偄傞偺偐丄幚嵺偵儘乕僇儖偐傜夋柺偵昤夋偝傟傞傑偱偺僾儘僙僗偱妋偐傔偰傒傞偲傛乣乣偔傢偐傝傑偡丅挿偄椃偵弌敪偱偡丅
丂傑偢丄儘乕僇儖嵗昗偵偁傞捀揰偼丄朻摢偱弌偰偒偨傛偆偵(x,y,z,w=1)偱掕媊偝傟傑偡丅崱丄偙偺捀揰偵儚乕儖僪曄姺峴楍傪妡偗嶼偟偰傒傑偡丗
丂峴楍拞偺乽m乿偲偄偆偺偼僗働乕儖偲夞揮偺梫慺傪娷傓晹暘偱偡丅偙偺晹暘偩偗偱偡偲丄儘乕僇儖嬻娫偵偁傞捀揰偼尨揰傪拞怱偲偟偨夞揮偐僗働乕儖曄壔偟偐偱偒傑偣傫丅偮傑傝丄偙傟偩偗偱偡偲僉儍儔僋僞偼尨揰偱僕僞僶僞偟偰偟傑偆傢偗偱偡丅偟偐偟丄w惉暘偑偁傞偲榖偼堘偄傑偡丅妡偗嶼偺寢壥傪尒傞偲乽1*Ofs乿偲偄偆晹暘偑w=1偲偡傞帠偵傛偭偰壛偊傜傟偰偄傞偺偑傢偐傝傑偡丅偙偙偼乽暯峴堏摦惉暘乿丄偮傑傝儚乕儖僪嬻娫偺岲偒側埵抲偵堏摦偱偒傞梫慺偵側偭偰偄傑偡丅
丂儘乕僇儖嵗昗偱w=1偲偡傞偺偼丄傕偆偍暘偐傝偺傛偆偵丄儚乕儖僪嬻娫偱暯峴堏摦傪偟偨偄偑偨傔偵愝掕偝傟偰偄傞晹暘側傫偱偡丅偙傟偑偁偭偰弶傔偰丄僉儍儔僋僞偼儚乕儖僪嬻娫撪傪摦偒夞傞偙偲偑偱偒傞乮傾僼傿儞曄姺偑偱偒傞乯傫偱偡両w=1偼偲偭偰傕戝愗側愝掕抣側傫偱偡偹丅
丂偝偰丄儚乕儖僪嬻娫偵堏摦偟偨捀揰偺嵗昗偺w惉暘偼憡曄傢傜偢1偱偡丅師偵丄偙偺捀揰偵價儏乕峴楍傪妡偗嶼偟傑偡ゥ葌駛艂穫獊A價儏乕峴楍偲偄偆偺偼捀揰傪僇儊儔偺慜偵帩偭偰偔傞乽曄姺峴楍乿偵夁偓傑偣傫丅梫偼忋偲摨偠傛偆側惉暘峔惉偺峴楍偵側偭偰偄傞偺偱丄寢壥偼扨弮偵丄
偲側傝傑偡丅枹偩w偼1偺傑傑偱偡丅
丂偙偙偐傜偑杮斣偱偡丅懕偄偰偙偺價儏乕嬻娫偵偁傞捀揰偵幩塭曄姺峴楍傪妡偗嶼偟傑偡丅偙偺幩塭曄姺峴楍偑旕忢偵娞偲側傝傑偡偺偱丄徻偟偔愢柧偟傑偡丅幩塭曄姺峴楍偼師偺傛偆偵掕媊偝傟偰偄傑偡丗
丂偙傟偼愭傎偳傑偱偺儚乕儖僪曄姺峴楍側偳偲偼條巕偑堘偄傑偡丅惉暘拞偺Sw傗Sh偼僗僋儕乕儞偺暆偲崅偝傪昞偟偰偄傑偡丅偙傟偼幚偼嬤暯柺偺僒僀僘偲摨偠偲掕媊偝傟偰偄傑偡丅
丂Zn偼嬤暯柺傑偱偺嫍棧偱偡丅Q偲偄偆偺偼價儏乕嬻娫偵偁傞捀揰偺Z惉暘偵懳偡傞僗働乕儖偱偡丅偳偆偄偆僗働乕儖抣偵側傞偺偐偼屻弎偟傑偡丅_43惉暘偺-QZn偼Z幉曽岦傊偺僆僼僙僢僩偱偡偹丅偦偟偰撍弌偟偰偄傞偺偑_34惉暘偺乽1乿丅偙傟偑娞偱偡丅
丂偙偺傑傑奺惉暘傪挱傔偰偄偰傕丄壗傪偟偨偄偺偐偪偭偲傕椙偔傢偐傜側偄偲巚偄傑偡偺偱丄愭傎偳偺價儏乕嬻娫偵偁傞捀揰Pview偵偙偺峴楍傪幚嵺偵妡偗嶼偟偰傒傑偟傚偆丗
丂暋嶨偦偆側姶偠偵側傝傑偟偨偑晐偔偁傝傑偣傫丅偙傟偑壗傪堄枴偡傞偐傪峫偊傞偨傔丄椺偊偽丄(Xview,
Yview, Zview)=(-Sw/2, -Sh/2, Zn)偲偄偆價儏乕嬻娫撪偺1偮偺嵗昗傪戙擖偟偰傒傑偟傚偆丅偪側傒偵丄偙偺嵗昗偼嬤暯柺偺嵍壓偺揰偱偡丗
XY惉暘偦傟偧傟偑-Zn丄偦偟偰Z偑0丅壗偲側偔嬤暯柺偺嵍壓偲寢壥偑僔儞僋儘偟偰偄傞婥偑偟傑偣傫偐丠
丂懠偺揰偱傕帋偟偰傒傑偡丅崱搙偼堦斣墦偄偲偙傠偵偁傞墦暯柺偺嵍壓偺嵗昗揰偵偟偰傒傑偡丅墦暯柺傑偱偺嫍棧傪Zf偲偡傞偲丄XY嵗昗偼師偺恾偵帵偡傛偆偵媮傔傜傟傑偡丗
Zn偲Zf偺斾棪傪巊偊偽媮傑傞傢偗偱偡丅偙偺恾偐傜丄Xview = -Sw/2 * Zf/Zn 偦偟偰Yview
= -Sh/2 * Zf/Zn偱偁傞偙偲偑傢偐傝傑偡丅偙傟傪Pproj偺幃偵偳乣傫偲戙擖偡傞偲丄堦斣墦偄暯柺偺嵍壓偺Pproj偼丄
丂
偲側傝傑偡丅崱搙偼XY惉暘偑-Zf偲側傝傑偟偨丅傗偭傁傝壗偲側偔墦暯柺偺嵍壓偲僔儞僋儘偟偰偄傞婥偑偟傑偣傫偱偟傚偆偐丠偨偩丄Z惉暘偼偙偺尒偨栚偱偡偲壗偲傕尵偊側偄姶偠偱偡丅偙偙偼僇儊儔偐傜堦斣墦偄埵抲偵偁傞傢偗偱乽Zf乿偵側偭偰梸偟偄傫偱偡丅偦偙偱丄Q傪師偺傛偆偵偟傑偡丗
偙偆偡傞偲Proj偼丄
偲側傝傑偡丅偐側傝旤偟偔懙偭偰偄傑偡偹丅
丂偦偟偰拲栚偺乽w乿丅偙偙偵偼價儏乕嬻娫偵偁偭偨捀揰偺Z惉暘偑偦偺傑傑棃偰偄傑偡丅偙傟偼Pproj偺w惉暘偺幃傪尒傟偽柧傜偐偱偡偹丅傕偆w偺堄枴崌偄偑尒偊偰巇條偑柍偄忬懺側傫偱偡偑丄偙偺w偼乽帇悕戜偺奼戝棪乿傪昞偟偰偄傞傫偱偡両両僇儊儔偐傜捀揰偑墦偗傟偽墦偄傎偳丄偮傑傝Z惉暘偑Zf偵嬤偯偗偽嬤偯偔傎偳w偺抣偼偦傟偵斾椺偟偰戝偒偔側傝傑偡丅
丂w偑帇悕戜偺奼戝棪側偺偱偡偐傜丄慡惉暘傪w偱妱傞偲偳偆側傞偐丠嬤暯柺媦傃墦暯柺偼偦傟偧傟偙偆側傝傑偡丗
旤偟偄両両椉曽偲傕XY惉暘偑摨偠偱Z偑堦斣嬤偄0媦傃堦斣墦偄1偲側傝傑偟偨丅偮傑傝丄偙偺忬懺偱僇儊儔偐傜尒傞偲乮亖僗僋儕乕儞偵搳塭偡傞偲乯椉曽偺捀揰偼廳側偭偰尒偊傞帠偵側傝傑偡丅嬤暯柺傕墦暯柺傕僇儊儔偺拞偵傄偭偨傝擺傑傞暯柺乮偦傟偑帇悕戜偺堄枴崌偄乯側偺偱丄偙傟偼棟孅偳偍傝偵側偭偰偄傑偡傛偹丅
丂偲偄偆帠偱寢榑偱偡丅w偼幩塭嬻娫乮帇悕戜嬻娫乯偵偁傞捀揰嵗昗傪偦傟偱妱傞偙偲偵傛傝乽捀揰傪僗僋儕乕儞偵搳塭偡傞偨傔偺棫曽懱偺椞堟乮-1亝x亝1丄-1亝y亝1偦偟偰0亝z亝1乯偵擺傔傞乿偲偄偆戝愗側栶栚傪偟偰偄傑偡丅w偑乽摨師宯乿偲屇偽傟傞偺偼丄忋偺椺偺傛偆偵帇悕忬偵僇儊儔偺帇慄曽岦偵峀偑偭偰偄傞捀揰傪摨偠XY嵗昗偵搳塭偡傞偨傔偱偡丅
嘇 捀揰僔僃乕僟偵擖偭偰偔傞捀揰嵗昗偲w惉暘偺峴偔枛
丂捀揰僔僃乕僟偵偼儘乕僇儖嵗昗偵偁傞捀揰偑偦偺傑傑擖偭偰偒傑偡乮POSITION僙儅儞僥傿僋僗乯丅僗僋儕乕儞偵億儕僑儞傪搳塭偝偣傞偨傔偵丄巹払偼偙偙偱儘乕僇儖嵗昗偺捀揰偵儚乕儖僪價儏乕幩塭峴楍乮WVP峴楍乯傪妡偗嶼偟傑偡丅偦偟偰丄偦傟傪捀揰僔僃乕僟偺弌椡捀揰偲偟偰弌椡偟傑偡乮POSITION僙儅儞僥傿僋僗乯丅偙傟偱儌僨儖偼偪傖傫偲夋柺偵弌傑偡丅嘆偱挿乆偲弎傋偰偒偨傛偆偵丄儘乕僇儖嵗昗偵偁傞捀揰偵WVP峴楍傪妡偗嶼偡傞偲丄w偱妱傞慜偺帇悕戜嬻娫撪偺捀揰嵗昗偵側傝傑偡丅偮傑傝丄捀揰僔僃乕僟偺弌椡捀揰嵗昗偼丄帇悕戜嬻娫撪偺嵗昗偩偭偨傫偱偡丅
丂捀揰僔僃乕僟傪敳偗偨捀揰偼偦偙偱弶傔偰w偱妱傝嶼偝傟丄僗僋儕乕儞偺搳塭埵抲偑妋掕偟丄偳偺揰傪慂偮傋偒偐寛傔傜傟偰僺僋僙儖僔僃乕僟偵忣曬偑揱傢傝傑偡丅偨偩偟丄僺僋僙儖僔僃乕僟偱偼偡偱偵慂偮揰偺忣曬傪捈愙庢摼偱偒側偔側偭偰偄傑偡丅偮傑傝丄偙偙偱w偼偍栶屼柶偲側傞傢偗偱偡丅
丂DirectX媄弍曇偦偺43乽Z抣傪僥僋僗僠儍偵彂偒崬傓揝斅側曽朄乿偱丄帺暘偱怺搙僥僋僗僠儍傪嶌傠偆偲偡傞帪偵丄捀揰偺Z嵗昗傪W抣偱妱傞偲偄偆嶌嬈偑昁梫偩偲偦偺復偺嘇偺偪傚偭偲忋曈傝偱帵偟傑偟偨丅偙傟偑側偤昁梫偐丄偙偙傑偱偺棳傟傪偛棟夝捀偗傟偽擺摼偟偰捀偗傞偲巚偄傑偡丅晄巚媍側w惉暘偺惓懱偼丄僗僋儕乕儞偵奊傪弌偡偨傔偵昁恵偺乽奼戝棪乿偩偭偨丅偙傟偱丄傕傗傕傗傕夝徚丄偡偭偒傝怮傜傟傑偡(^-^)丅