その57 クォータニオンを"使わない"球面線形補間

その57 クォータニオンを"使わない"球面線形補間

　3Dゲームを作る時に「補間」が出てくる場面がいくつかあります。例えば、キーフレームアニメーションをする時に行列Aから行列Bに滑らかに遷移させる時に補間が使われます。またいわゆる「アルファブレンド」は補間の代表ですね。行列間の遷移やアルファブレンドで使われる補間は「線形補間」と言います。

　一方補間には「球面線形補間」という補間方法もあります。これは2つの値の間を線形ではなくて球面上を沿うように補間する方法です。形式的には2つの同じ長さのベクトル間を円弧を描くように補間する方法を言う事が多いです。この補間方法は2つの姿勢間を滑らかに遷移させるのに活躍しています。

　球面線形補間を簡単にする方法として「クォータニオン」があります。クォータニオンで開始姿勢と終了姿勢を表してD3DXQuaternionSlerp関数に渡すと、その中間姿勢となるクォータニオンを自動的に算出してくれます。とても簡単です。でも、でもです、「開始姿勢を表すクォータニオン」って、簡単に作れるでしょうか？例えば、(20,15,30)という位置で(100,120,-50)を向いているUpベクトルが空方向のカメラの姿勢をクォータニオンでさっと表すのはちょっと難しいと思うんです。つまり、せっかくD3DXQuaternionSlerp関数があっても、姿勢を表すクォータニオンをうまく作れないのならば意味が無いわけです。

　ある姿勢を表すのであれば、姿勢行列を使う方が抜群に簡単です。ワールド空間でのオブジェクトの3軸（XYZ）の方向さえわかれば良いのですから。であれば、この3軸を使った球面線形補間があれば、わざわざクォータニオンを持ち出す事はなくなります。

　そこで本章では、あえてクォータニオンを使わずに3軸による球面線形補間で2つの姿勢間を補間する方法を試行錯誤してみたいと思います。

① 補間の一般式

　補間と言うのは最終的にAからBに値が移れば良いだけです。そこで、次のような一般式が成り立ちます：

太文字は値です。Sはスタートの値、Eはエンド（ゴール）の値です。また、P_SとP_Eという2つの関数がありますが、これは次のような性質を持っているとします：

tは媒介変数と言って、スタート時を0、ゴール時を1として0→1と値を変える事で「どの中間値を算出して欲しいか」を指定する事ができます。つまりP_Sはt=0、すなわちスタート地点で1となりゴール地点で0になる関数です。P_EはP_Sと逆の動きをして、スターと地点で0で、ゴール地点で1になってくれる関数です。実際、補間の一般式でt=0の時は結果はSに、t=1の時はEになるのが確認できますよね。

　さて、「じゃあ具体的にP_SとP_Eにはどんなのがあるんさ？」となりますが、簡単なのはアルファブレンドなどで使っている次の式です：

先の性質を持っていますね。この関数を持った補間は「線形補間」と呼ばれています。なぜ「線形」なのか？それは次のグラフを見れば一発です：

青いグラフが上のP_SとP_Eです。他のグラフは別の関係を作ってみたものです。唯一青いグラフだけが直線ですね。StartからEndまで真っ直ぐに進める補間は線形補間以外ありません。

② 球面補間

　普通補間をする場合は「条件」を付けたくなります。良くあるのが「点の間を等速で歩きたい」という条件。これを満たす簡単な補間は線形補間です。他にも「次の点までスムーズに繋げたい」とか「エネルギーのロスを少なくしたい」など、色々あるわけです。

　そんな中で次のような補間をしたい事があります：

Startにある点を「原点で回転させて」Endに持っていきたい。これはStartからEndまでの「球面補間」と呼ばれています。

　上の図を地球を輪切りにしたと考えてみます。原点が地球の中心です。地表のどこかにStart（出発地点）とEnd（目的地）があって、目的地に向かって真っ直ぐ歩くと図のような軌跡を描く事になります。この時、歩いた人の感覚だと真っ直ぐ歩いているのですが、3次元で見れば図のように曲がっていますよね。こういう歩き方ができる補間を作ってみます。

　実際作るのは簡単です。話を簡単にするためにベクトルSやEの長さを1だとします。StartからEndに向けて線を引きます。この線上のどこかの点に向かうベクトルは、先の線形補間を使えば簡単に求まります。その補間ベクトルをIとします。後はこのIを球面まで引き伸ばします。要は「正規化（Normalize）」をすれば良いのでD3DXVec3Normalize関数にIをかければ長さが1になります。これで、球面上を沿う補間が出来てしまうんですね：

伸ばせば出来る球面補間！

　ただし、これは「球面補間」です。感覚的にわかると思いますが、線上にあるtを等速で増やしていっても球面上は等速にはなりません。

　地球の上を同じ速度で歩く、つまり球面上を等速で動かすには、線上のtの速度をそうなるように調節する必要があります。ではどう調節するのか？これが球面線形補間の肝となります。

③ 球面"線形"補間

　球面上を線形に補間する方法を考えるために次の図をご覧下さい：

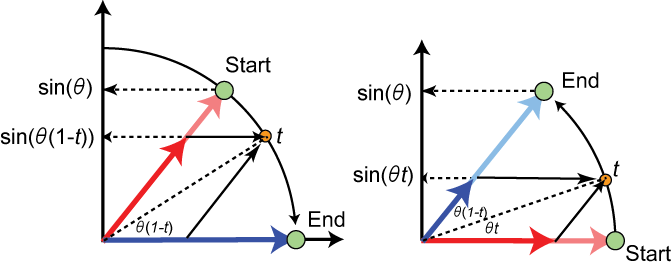
　うわ～って思うかもしれませんが大丈夫です。

　左の図から説明します。円弧がありますね。これがStartからEndに向かう補間軌道です。この補間軌道上を等速で移動するためには、角速度一定、すなわちtθで角度が変化すれば良いわけです（θはStartベクトルとEndベクトルの成す角度）。起動上にあるオレンジの点は補間中の点で、媒介変数tでその位置が確定します。tでの位置をStartベクトルとEndベクトルで表現するには「ベクトルの合成」を利用します。

　端的に言えば、tを指している軸に平行なベクトルを足せば、その合成ベクトルはtを指すベクトルとなります。まずはStartベクトル側から見ていきましょう。Startの方向を向いた濃い赤矢印が薄い赤矢印より短くなっています。合成するためにこの長さのベクトルにする必要がありますよ～という意味です。濃い赤矢印のベクトルの長さは、Y軸に示してあるsin値の比で求められます。Start地点の高さはsin(θ)です。それに対して赤いベクトルの高さはsin(θ(1-t))となります。薄い矢印のベクトルは単位ベクトルにしていましたので長さは1。よって、赤いベクトルの長さは、

と比例計算で出てきます。

　さて一方の右図ですが、これはEnd側について同様の比例計算をしてみようと左図と同じアングルにしてみたものです。薄青の矢印を濃青矢印まで縮めるのが目的です。左図と同様に、End地点での高さはsin(θ)、位置tでの高さはSin(tθ)です。全く同じようにして比例計算すると、

となります。以上からあるtに対する補間位置Iは、

とベクトルの合成で計算できます。これ、補間の一般式そのものになっていますよね(^-^)。

④ 計算に必要な物

　理屈がわかった所で、実際の計算に必要な物を揃えます。

　まずはStart地点及びEnd地点となるベクトルです。このベクトルは正規化して単位ベクトルにしなければなりません。続いて両者の間の角度です。これは2つのベクトルの内積から出るcosθをacos関数に放り込むと出てきます。媒介変数tの値はもちろんプログラマが与えます。

　以上を踏まえた球面線形補間関数を公開致します：

球面線形補間算出関数

// 球面線形補間関数 // out : 補間ベクトル（出力） // start : 開始ベクトル // end : 終了ベクトル // t : 補間値（0～1） D3DXVECTOR3* SphereLinear( D3DXVECTOR3* out, D3DXVECTOR3* start, D3DXVECTOR3* end, float t ) { D3DXVECTOR3 s, e; D3DXVec3Normalize( &s, start ); D3DXVec3Normalize( &e, end ); // 2ベクトル間の角度（鋭角側） float angle = acos( D3DXVec3Dot( &s, &e ) ); // sinθ float SinTh = sin( angle ); // 補間係数 float Ps = sin( angle * ( 1 - t ) ); float Pe = sin( angle * t ); *out = ( Ps * s + Pe * e ) / SinTh; // 一応正規化して球面線形補間に D3DXVec3Normalize( out, out ); return out; }

　使い方はとっても簡単です。startに開始ベクトルを、endに終了ベクトルを入れて、補間値tを指定するとoutに補間ベクトルが戻ってきます。

⑤ 球面線形補間は姿勢を保つか？

　球面線形補間によって2つのベクトルがその長さを保ったまま回転補間できるようになりました。線形補間と違ってベクトルの大きさが変わらず、また回転速度が一定なのも魅力です。

　この球面線形補間でキャラクタやカメラの姿勢を制御するのも魅力です。特に空中を縦横無尽に飛び回るカメラの姿勢を制御するにはこういう補間が大変に役に立ちます。

　しかしです。姿勢を制御するにはキャラクタやカメラにくっついている3つの軸（XYZ）について、

･各軸のベクトルの長さが1に保たれる事
・各軸の直交性が保たれる事

という2つの性質、すなわち「正規直交性」が保たれる事が条件になります。この内一番目の条件については保証されています（長さを必ず1にしているので）。では2番目の直交性はどうか？これは確かめないといけません。これを確かめるには正規直交な2つの行列の中間行列を作り、その直交性をテストするのが一番です。

　そこで2DのXY軸をワールドに2つ置き、一方をStartもう一方をEndとして、各軸を独立に球面線形補間してみました。補間中の軸の内積を計算すれば、直交しているかどうかがわかります。その数値結果はこちら：

t dot degree

0 0.00 90.0

0.1 -0.11 96.2

0.2 -0.19 101.2

0.3 -0.25 104.5

0.4 -0.27 105.9

0.5 -0.27 105.4

0.6 -0.23 103.3

0.7 -0.18 100.1

0.8 -0.11 96.4

0.9 -0.05 92.8

1 0.00 90.0

ん～～、degreeを見ると補間開始のt=0及び補間終了時のt=1の時は90度ですが、その他の補間中では90度以外になっているので、残念ながら球面線形補間で軸の直交性は保障されないようです。つまり、3つの軸を独立に球面補間すると姿勢は保てない事がわかりました。

　さてではどうするか？次のように考えて見ます。姿勢を決定するには2軸で十分です。すなわちカメラで言えば視線の方向に当たるZ軸と、カメラの上方向に当たるY軸があれば姿勢は保てます。そこで、両方のベクトルを球面線形補間で補間します。ただしそのままでは直交性を保てないので、補間後のZ軸をまずは採用し、続いてYZ軸から一度直交するX軸を求め（外積）、最後にXZ軸から直交Y軸を計算し直します。これで姿勢として成立します。

　この姿勢補正を行った球面線形補間による姿勢補間関数を公開します：

球面線形補間による姿勢補間関数

// 球面線形補間による補間姿勢算出関数
// out : 補間姿勢（出力）
// start : 開始姿勢
// end : 目標姿勢
// t : 補間係数（0～1）
D3DXMATRIX* CalcInterPause( D3DXMATRIX* out, D3DXMATRIX* start, D3DXMATRIX* end, float t ) {

// 各姿勢ベクトル抽出
D3DXVECTOR3 Sy, Sz;
D3DXVECTOR3 Ey, Ez;

memcpy( &Sy, start->m[1], sizeof( float ) * 3 );
memcpy( &Sz, start->m[2], sizeof( float ) * 3 );
memcpy( &Ey, end->m[1], sizeof( float ) * 3 );
memcpy( &Ez, end->m[2], sizeof( float ) * 3 );

// 中間ベクトル算出
D3DXVECTOR3 IY, IZ;
SphereLinear( &IY, &Sy, &Ey, t );
SphereLinear( &IZ, &Sz, &Ez, t );

// 中間ベクトルから姿勢ベクトルを再算出
D3DXVECTOR3 IX;
D3DXVec3Cross( &IX, &IY, &IZ );
D3DXVec3Cross( &IY, &IZ, &IX );
D3DXVec3Normalize( &IX, &IX );
D3DXVec3Normalize( &IY, &IY );
D3DXVec3Normalize( &IZ, &IZ );

memset( out, 0, sizeof( D3DXMATRIX ) );
memcpy( out->m[0], &IX, sizeof( float ) * 3 );
memcpy( out->m[1], &IY, sizeof( float ) * 3 );
memcpy( out->m[2], &IZ, sizeof( float ) * 3 );
out->_44 = 1.0f;

return out;
}

　引数のstartとendに適当な姿勢が入った行列（これはワールド変換行列なども可能です）及び補間値tを入れると、その間の球面線形補間姿勢をoutに返してくれます。簡単です。

⑥ クォータニオンを使わない理由

　ここまでクォータニオンを使わずに姿勢を球面線形補間で制御する方法を見てきました。クォータニオン自体は素晴らしい数学的手法です。回転に関して直感的だとも言われます。しかし、良く知らずに使って悪戯に混乱を招いてる面もあります。

　今回あえてクォータニオンを使わずに姿勢補間を考えたのも、実はカメラの姿勢制御をしようと思ったのがきっかけです。球面線形補間ならクォータニオンだろうと思ったら、クォータニオンでそのカメラ自体の姿勢を現す方法が良くわからない･･･。姿勢を表せたとして、カメラは未だ4×4行列で表現されていて、それを一度クォータニオンに変換して補間して行列に戻して･･･と、何とも遠回りに感じました。

　本章で作った補間関数なら、行列から行列へストレートに姿勢を補間できます。このままですと2つの姿勢間の補間で終わってしまいますが、工夫次第できっと次の点も見据えてカメラをよりスムーズに動かす事もできるかなと想像します。その辺りも今後考えていければなと思います。

t	dot	degree
0	0.00	90.0
0.1	-0.11	96.2
0.2	-0.19	101.2
0.3	-0.25	104.5
0.4	-0.27	105.9
0.5	-0.27	105.4
0.6	-0.23	103.3
0.7	-0.18	100.1
0.8	-0.11	96.4
0.9	-0.05	92.8
1	0.00	90.0