ホーム < ゲームつくろー! < DirectX技術編
その60 変換行列A×BとB×Aの違いを知ろう
3Dのゲームを作る上で変換行列は欠かせません。ローカルにあるモデルを世界に置くにはワールド変換行列が必要です。ところで、そのワールド変換行列を作る過程で「行列の掛け算」が出現します。例えば回転行列Rと位置行列Tから「30度回転させて座標(10,20,30)にモデルを置くワールド変換行列」なるものを作るわけです。
では、「世界に置いた位置からさらにモデルの向いている方向に40だけ移動させるワールド変換行列」とか「親モデルから相対的に30度親の空間のZ軸で回転させる」などゲーム制作上必要となる複雑なワールド変換行列を作るにはどう考えてどう行列を掛け算をしていけば良いのでしょうか。この行列感覚はとてつもなく重要です。
本章では色々な事例を検証しながら「変換行列を掛ける」という事をどう捉えるべきか見ていきたいと思います。
① 検証1:ローカルのモデルに行列を掛けるとはどういう事か?
モデルは自分の空間(ローカル空間)に存在します。もう少し具体的に言うと、モデルのポリゴンを構成する「頂点座標」の値がローカル空間の座標系で表現されています。このモデルに対して座標変換行列Mを適用します。すると、このモデルの頂点座標は何らかの別の位置に移動します。
座標変換行列Mには「回転」「移動」「スケール」などがあり(他にもあります)、それらを連続的に掛け算していくことでモデルを特定の姿勢にして世界に置きます。ここで問題。「Y軸中心で30度だけ回転する行列M1」があるとし、そこにさらに「Z軸中心で回転する行列M2」を掛けるとモデルは、
A. Y軸で30度回転した世界のZ軸
B. Y軸で30度回転したモデルのZ軸
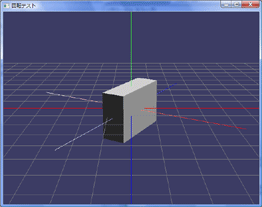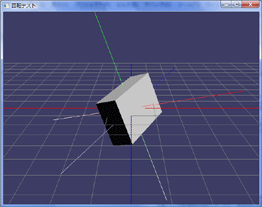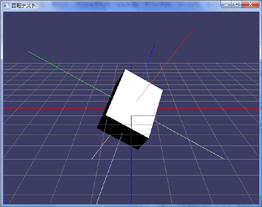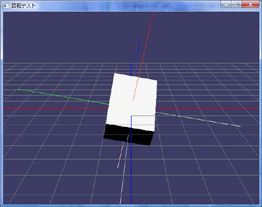
のどちらを軸として回転するでしょうか?これを実際にやってみます:
うわ、GIFアニメーションだと分かりにくい・・・(-_-;。
グリッドはワールド、Boxに刺さっているのがBox自体のローカル軸です。良く見ていただくとY軸で30度回転しているBoxがグリッドの青い軸(Z軸)を中心にさらに回っているのがわかると思います。つまり答えは「A」の世界のZ軸で回転するです。
DirectXの行列形式では、右へ右へと座標変換行列を掛け算していくと、それらは全て変換先に考えている世界の座標系を基準とする事になります。ですから、モデルを自分自身の正面方向に移動(モデルの回転後のZ軸方向へ移動)させようと思っても、行列を右へ掛け算してしまうと自分の軸は考慮されないため、思うように動かせません。
では、モデルをY軸中心で30度だけ回転させ、さらに「回転後のモデルのZ軸を中心に回す」にはどうしたら良いのでしょうか?実は、今度はY軸30度回転行列の左側にZ軸回転の行列を掛け算すると実現できてしまうんです:
上のアニメーションを見ると、今度はBoxのZ軸を回転軸として回っているのが分かると思います。行列を左へ掛けると、モデルの軸を基準として座標が変化します。
では応用問題。ワールドの(10, 0, 10)を中心としてXZ平面上を半径10で回転移動させつつ、自分自身のZ軸で自転させるにはどうしたら良いでしょうか?
まず回転運動はsinやcosを使ってこう表現できます:
float a = 0.0f; // <- 毎フレーム増加させます
D3DXMATRIX circleTrans;
D3DXMatrixTranslation( &circleTrans, 10.0f + 10.0f * cos(a), 0.0f, 10.0f + 10.0f * sin(a) );
// ↑ (10, 0, 10)のオフセットも入っていますよ
これをモデルに適用しaを増加させていくと、元の姿勢を保ったままワールド空間で(10, 0, 10)を中心に回転移動を行うようになります。次に自分自身のZ軸で自転させるために、Z軸回転行列を左に掛けます。すなわち、
D3DXMATRIX rotZ;
D3DXMatrixRotationZ( &rotZ, a );
D3DXMATRIX worldMat = rotZ * circleTrans;
というワールド変換行列を作成すると、モデルは仕様に沿った動作をするようになります。
もう1つ、ちょっと似た別の応用問題。同様にワールドの(10, 0, 10)を中心として半径10で回転移動をさせるのですが、今度はモデルのZ軸が常に中心点を向くようにして、さらにそのモデルのZ軸で自転させるにはどうするか?
これも少しずつ考えると分かります。まず、モデルのZ軸を回転の中心点に向かせるために、モデルをワールドのZ軸方向に-10だけ平行移動する行列を作ります:
D3DXMATRIX ZTrans;
D3DXMatrixTranslation( &ZTrans, 0.0f, 0.0f, -10.0f );
これをモデルに適用すると、モデルのワールド位置が(0, 0, -10)に移動します。次にワールド空間のY軸を回転軸として回転させます。つまりY軸回転行列を右に掛け算します:
D3DXMATRIX rotY;
D3DXMatrixRotationY( &rotY, a );
D3DXMATRIX worldMat = ZTrans * rotY;
これにより、モデルのZ軸が常にローカル空間の原点を向くような回転になります。仕様での中心点は(10, 0, 10)なので、さらにワールド空間の座標軸を基準としたオフセット行列を右に掛け算します:
D3DXMATRIX Offset;
D3DXMatrixTranslation( &Offset, 10.0f, 0.0f, 10.0f );
D3DXMATRIX worldMat = ZTrans * rotY * Offset;
これでワールド空間基準の移動・回転ができました。仕様ではさらに「モデルのZ軸を中心に自転」というのが入っています。モデルを基準にする時には行列を左に掛けるのですから、次のようにZ軸回転行列を左側に掛け算します:
D3DXMATRIX rotMyZ;
D3DXMatrixRotationZ( &rotMyZ, a );
D3DXMATRIX worldMat = rotMyZ * (ZTrans * rotY * Offset);
このワールド変換行列をモデルに適用すると仕様通りに動きます(^-^)。行列を作る感覚、掴めてきたでしょうか?
② 検証2:モデルの親子関係
2つのモデルPとQの間に親子関係を構築するという状況がゲーム製作で絶対に出てきます。例えばキャラクタが持っている武器はキャラクタの掌に握らせる必要がありますし、その武器に付属しているパーツは武器を原点として定義されるべきです。この時武器の親はキャラクタ、パーツの親は武器となります。
そういう親子関係をもう少し具体的に言うと、子は自分の親の空間の軸を基準として移動や回転を行います。さらに、子自体も自分の座標系を中心として移動・回転を行う場合もあります。①で検証した事を踏まえれば、親子関係を実現するには次のような行列の掛け算をすれば良いのがわかります:
[子のワールド変換行列] = [子のローカルでの移動・回転行列] × [親空間へのワールド変換行列]
これを実際に試してみます。親の空間(ワールド空間)でY軸30度回転させる行列の左からX軸平行移動行列を掛けてみるとこうなります:
親の空間の軸を基準に回転した後の自分の空間軸を基準として、自分のX軸上(Boxから伸びる赤い軸)をBoxが移動しているのがわかります。
親の空間を基準とした子の動きというと「ボーン操作」が真っ先に思い浮かびます。ボーンを動かす時、自分の姿勢行列の右側に基準となる親の姿勢(ボーン行列)を掛けます(DirectX技術編その27「アニメーションの根っこ:スキンメッシュアニメーション(ボーン操作)」④を参照)。これは上記のような変換行列の性質によるものだったというわけです。
この性質は逆に、「子がワールドを見る」という事をちょっと難しくします。それは、子の知っている世界が親の空間になってしまうためです。ですから、世界のある位置に子を移動させようと思うと、その位置を子と同じ親の空間にまで変換する必要が出てきます。こういう親→子という空間の逆遷移操作は例えばIK(インバースキネマティクス)で頻出します。
③ 検証3:あるモデルの世界へ連れ込む
衝突判定を行う時にモデルAの空間でモデルBを表現すると判定が楽になることがあります。例えばOBB(有向境界ボックス)と点の衝突をする必要があるとき、もちろんまともにもできますが、OBBの空間に点を移動させると問題が「AABB vs 点」になりより簡単になります。
連結したボーンの末端の動きに合わせて親ボーンの位置を操作するIK(インバースキネマティクス)では、目標とする点に末端ボーンを向ける操作が必須です。大抵の場合、末端ボーンの目標点はワールド空間にあります。しかし、末端ボーンの知っている世界は自分の親空間です。そのため、ワールド空間にある目標点を子の知っている親の空間まで移動させる必要があります。このようにある点や物を別の空間の座標で表現するという操作は3Dのゲームを作る上でかなり頻繁に出てきます。
ローカル空間にあるモデルAはワールド変換行列を掛ける事で世界へ置かれます。これを式で表すと次の通りです:
[ワールド空間のモデル(頂点)] = [ローカル空間のモデル(頂点)] * [ワールド変換行列]
この式の両辺にワールド変換行列の逆行列を右から掛けてみます。すると、
[ワールド空間のモデル(頂点)] * [モデルのワールド変換逆行列] = [ローカル空間のモデル(頂点)]
* [モデルのワールド変換行列] * [モデルのワールド変換逆行列]
[ワールド空間のモデル(頂点)] * [モデルのワールド変換逆行列] = [ローカル空間のモデル(頂点)]
結果、ローカル空間のモデルが右辺に残りました。つまり、ワールドにあるモデルにワールド変換行列の逆行列を右から掛けるとローカルの空間に戻されるわけです。よって、ワールドにあるあらゆるものは、ある特定のモデルの空間に簡単に移すことが可能です。
ここで一つ問題。モデルAとBがそれぞれのローカル空間で定義されているとします。モデルBをAの空間に移すにはどうしたら良いでしょうか?
これは下の図を見て頂くと簡単です:
モデルAを世界に置くにはWAを適用します。同様にモデルBはWBを掛ける事で世界に置かれます。よって、WBでモデルBを世界に置いた後に、WA-1でモデルAの世界に戻せば良いんです。つまり、赤い矢印の順番で行列を右に掛け算していきます:
[モデルAの世界でのB] = [モデルB] * WB * WA-1
上のような空間の関係図を描くと、例えば射影空間にあるモデルBをモデルAのローカル空間に戻すにはどうするか、スクリーン空間で定義した線分とワールド空間のモデルとを衝突させるにはどうするかなど、視覚的にわかるようになります。
次に親子関係のあるモデル(空間)について考えてみましょう。2つの空間PとQが親子関係、つまりPの中にQが包含されている状態だとします。実はこの関係、上の図の「World」と「Model」の関係そのものである事にお気付きでしょうか?親であるPがWorld、子QがModelにそれぞれ対応するわけです。よって、子であるQをPの空間の軸を基準に動かすには、Qのワールド変換行列を作れば良いわけです。
この親子関係をもうちょっと拡張してみます。Qの子にR1とR2がいるとしましょう。これらの関係を図に描くとこうなります:
この図が描けるともう勝ったも同然です。R1にとってみればQがワールドです。よってQの空間に自身を置くにはその変換行列WR1を自分に掛けてあげれば良くなります。Qにある物(モデル)をPに置くには、その変換行列WQをモデルに掛ければOKです。という事は、R1をPの世界に置くには、
[モデルR1のワールド姿勢] = [モデルR1] * WR1 * WQ
と行列を掛け算すれば良いのがわかります。右へ右へと親の空間への変換行列を掛け続ければ、どれだけ連鎖が長くても一番偉い親の空間に所属する全ての子を移す事ができます。
では上の図を踏まえて問題。Pの世界にある物をR1の世界に移すにはどうするか?まぁ、もう言うまでも無いですね(^-^;。上の図の青い矢印の通りにPの世界にある物に逆行列を右へ掛けて行けばR1の世界に移ります:
[モデルR1の世界で見たモデル] = [Pにあるモデル] * WQ-1 * WR1-1
= [Pにあるモデル] * ( WR1 * WQ )-1
気を付けたいのが逆行列の掛ける順番です。上の図の矢印の向きの通りに掛ける必要があります。ただ、下の式の右辺で括弧でくくった行列に注目です。この中は子から親へ行列を掛け算しています。これは逆行列にある次の性質を利用しています:
M1-1 * M2-1 * M3-1 * ... = (... * M3 * M2 * M1 )-1
もう1問。上の図だと変換行列WR1はモデルQの軸が基準となります。つまりモデルQの世界の軸を元に回転や移動が行われるわけです。でも、例えばモデルR1が向いている方向に進み続けたいとか、モデルR1は自身のX軸でしか回転できない(回転制約)など、R1の世界で移動や回転を考えたい時が結構あります。では、モデルPの世界に移したR1を、R1自身の空間で移動回転させるにはどうしたら良いでしょうか?
ここまで読み進めて頂いていればこの問題ももう簡単です。①で検証したように、ローカル空間での移動や回転を行うには、ワールド変換の左側に変換行列を掛ければ良いのでした。つまり、
[モデルR1のワールド姿勢] = [モデルR1] * LR1 * WR1 * WQ
とLR1を先に掛け算すると望む姿勢変換が可能になります。
これをもう少し一般化してみます。自分の親の世界へ移す行列をW、自分の世界での移動や回転を表す行列をLとすると、行列の掛け算を次のように汎用に書く事ができます:
WMは最終的なワールド変換行列、Liはモデルiのローカル変換行列、Wiはモデルiのワールド変換行列、Πは「順番に全部掛け算しなさい」という記号です。括弧でくくっている行列がそのモデルの姿勢行列になっています。注意したいのは、自分を一番最初に、次に自分の親、さらにその親という順番で行列を掛け算する必要があるという点です。そのため下式のΠ内にある行列の添え字が(n-i)となっています。
この式の関係図は次のように一般化して描けます:
この図がゲームでの行列変換のほぼすべてを物語っていると言っても良いかと思います。
先の式を擬似プログラムで書くと、自分の姿勢行列(ワールド変換行列)を更新するメソッドが例えばこんな感じで書けます:
void Model::updateMatrix( const D3DXMATRIX &parentMatrix ) {
// worldMatrix : 自分のワールド変換行列
// localMatrix : 自分の軸を基準とした動き
// worldMatrixToParent : 親の軸を基準とした動き
// parentMatrix : 親のワールド変換行列
worldMatrix = localMatrix * worldMatrixToParent * parentMat;
// 自分の子の姿勢を更新
for ( int i = 0; i < numChild; i++ )
childrenModelArray[i].updateMatrix( worldMatrix );
}
引数に自分の親の姿勢行列が来るので、それを使って自分の姿勢を更新しています。さらに自分に登録されている子供に自分の姿勢を渡します。これにより、一番上の親のupdateMatrixを呼ぶと末端まで姿勢更新が伝播していきます。
この考え方はボーンによる姿勢更新に直結します。例えば、世界のある崖の上に立っているキャラクタの耳についているイヤリングを「イヤリングのZ軸回転」で揺らす必要がある時どういう変換作業が必要か、先の式に従うとこうなります:
[イヤリングのワールド変換行列] = [イヤリングモデル] * { L(Z軸回転) * W(頭部に対する変換行列) * ...(キャラクタの一番上の親まで掛け算)... } * L(キャラクタ自身の軸での変換行列) * W(世界に対する変換行列)
大括弧はボーン操作、そこから先はモデル操作になっています。こう見ると、ボーン自身も一つのモデル(モデルクラス)として扱うと、姿勢のすべてを同じ処理方法で管理できますよね。
④ 検証4:スクリーン視点でモデルを動かす
例えばスクリーン座標まで変換するいつもの変換作業を図示するとこうなります:
長い・・・(^-^;
この図があれば、モデルをスクリーンにまで変換するのはもう簡単ですし、スクリーンにある点をモデルやワールド空間に戻すのも楽々です。
ただ、実際にゲームを作っていると、「ビュー視点(カメラ視点)で見たキャラクタをビューの軸を基準として右や奥に動かす」という要求が大概の場合出てきます。それ以外にもスクリーン座標(軸)を基準にしてキャラクタを動かす必要があるかもしれません。一つ上の親ではなくて、もっと遠くにある親の軸を基準に子である自分を動かすには、ちょっと特殊な事をする必要があります。
①で検討したように、変換行列を右に掛けると、それは親となる空間の軸を基準とするのでした。例えばローカルにあるモデルをビュー空間にまで移動させる式は、
[ビュー空間のモデル] = [ローカル空間のモデル] * (LM * WM * VM)
です。括弧の中を一つの行列として考えると、この括弧の中は「ビュー空間への変換行列」とみなせます。よって、ビュー空間軸を基準としてさらに移動当を行うには、この式の右側にそれを表す変換行列を掛ければ良い事がわかります:
[ビュー空間のモデル] = [ローカル空間のモデル] * (LM * WM * VM) * MatrixInView
これでローカル空間にあるモデルはビュー空間の軸を基準に動くのですが、ただ、実際こういう行列の掛け算は実装上ちょっと採用し難いものがあります。なぜか?ゲームで扱う全てのモデルは大抵「ワールドにある」という前提がしかれているためです。それは操作可能な主人公キャラクタも例外ではありません。よって、主人公キャラクタだけが上式で「ビュー空間にあるモデル」として計算されてしまうと大変にまずいわけです。よって上の式の左辺は結果として「ワールド空間のモデル」になるべきなんです。ではどうするか?
答えは簡単です。ビュー空間にあるモデルをワールド空間に戻すには、そう「ビュー変換行列の逆行列」を右から掛け算すれば良いんです(上の図を見ても明らかですね)。という事で、上式はこう修正されます:
[ワールド空間のモデル] = [ビュー空間のモデル] * VM-1 = [ローカル空間のモデル] * LM * WM * { VM * MatrixInView * VM-1 }
ビュー変換行列はどこからか手に入れられるとして、いったんその空間に移動してその軸で動かした後「逆行列を掛けて空間を戻す」という作業を入れます。これによりシステムの整合性が保たれる事になります。一般に、自分をある空間の軸を基準として動かすには、いったん自分をその空間まで移動させて、その軸基準で動かした後、元の自分の空間まで戻すという作業が入る事が多いように思います。
⑤ まとめ
この章では色々な行列変換のシチュエーションを検証してきました。多くの場合③の最後に挙げたような空間の親子関係図があると、どういう変換をすべきかが直ぐにわかります。行列を左に掛けるのか右にかけるのか?それも自分の軸を中心に動かすのか親の軸を中心に考えるのかの違いで判断できます。
気を付けて欲しいのは、この章で検証した行列の掛ける方向は「DirectXの場合」である事です。OpenGLはDirectXの変換行列の転置行列が姿勢行列として採用されています。この場合、自分の空間の軸を基準とした変換をする場合は右側へ、親中心なら左側へ行列を掛け算します。DirectXと逆になるわけです。これを混乱してはいけません。
もう1つ、非常~~に気をつけて欲しい事。それは「右手系、左手系は関係ない」という事です。DirectXは左手系座標、OpenGLは右手系座標を採用しています。右手左手系というのは座標軸の方向性を定義しているだけで、これと行列の掛ける方向は全く関係しません。しかし、これが混同されて「右手系は右へ右へと掛け算、左手系は左へ左へ掛け算する」という感じの「系と掛ける方向」の間違いをよく耳にします。右掛けか左掛けかは、採用している姿勢行列が行中心か列中心かの違いに関係しています。DirectXは「左手系で行中心の行列を採用」、OpenGLは「右手系で列中心の行列を採用」しているので、掛ける順番が逆になっているだけです。右手系であっても行中心の行列を採用すれば、掛ける順番はDirectXと同じになります。
行列の掛け算、しっかり整理しておきたいですね。