ホーム < ゲームつくろー! < DirectX技術編
その63 DirectX9のスクリーンドット化(ラスタライゼーション)ルール
DirectXは三角形ポリゴンをベースとして描画が行われます。至って当然な気がしますが、よ~く考えてみると、次のような変換が必要になるのがわかります。
三角形ポリゴンの各頂点は浮動小数点(float)で表現されます。小数点は理屈上は連続な値です。その頂点が色々と数値変換されて、最終的にはスクリーン座標に変換されます。そのスクリーン座標は「整数」で、スクリーン上の点は厳密には小さな正方形です。整数はご存知不連続なものです。連続がいつの間にか不連続になっている事は、普段あまり気にしませんが実は重要です。
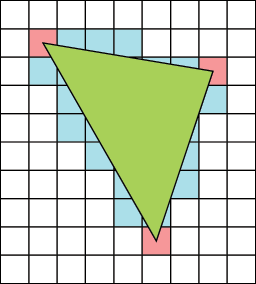
連続なポリゴンを不連続なピクセルに直すには何らかの仕組み(ルール)が必要です。そのルールのことを「ラスタライゼーションルール(Rasterization Rule)」と言います。例えば、今ポリゴンの3頂点のスクリーン位置が決まったとして、辺や中身はどう塗りつぶされるかを考えてみます:
辺を含んでいるどの青いセルが塗りつぶされるのか?もしかして全部塗りつぶされる?面積が多ければ塗りつぶされる?これがちゃんと決まっていないと見た目がぜんぜん変わってしまうわけです。これは特にスクリーンピクセルを意識した描画、例えば2DのHUDやポストエフェクトレンダリングなどに大影響を与えます。
この章ではそんな地味に大切ラスタライゼーションルールについて見ていこうと思います。尚、以下断りが無い限りポリゴンはスクリーンの範囲に数値が変換されているとします(ただし小数点です)。また矩形は画面のドットそのものです。
① スクリーンドットと頂点の位置関係
ポリゴンが色々な変換を経てスクリーンの範囲と同じ値になったとしましょう。ただし、値は浮動小数点のままです。この時、ポリゴンの小数点値とスクリーンのドットとは次のような位置関係になります:
オレンジの点がポリゴンが変換された小数点値、赤い数字がスクリーン座標点です(0基点なのに注意)。小数点の整数値(3.0とか)がドットのど真ん中に来ているのがポイントです。DirectXではこの「オレンジ色の点がポリゴン内に含まれていたら基本的には描画」というルールがまずあります。「基本的」というのは、それだけだと困った事が起こるためです。
例えば、4×4の小さなHUDを表示させようとする時、イメージする板ポリゴンは次のような頂点設定です:
当然ですね。これを上の位置関係図に当てはめてみましょう:
「!!!」。よく見ると縦横5ピクセルにまたがっています。4×4にしようと思ったら5×5?これはいったいなんじゃらほいなわけです。
もう一つ別の問題を。板ポリゴンに限らず、DirectXのポリゴンは三角ポリゴンです。上のポリゴンを三角形に分割するとどうなるか?
左下ポリゴンと右上ポリゴンの境界線はオレンジの点を両方共含んでいます。ということは、ここは2度塗りつぶされてしまいます。含んでいる部分を単に塗るという事だけでは色々と変なことが起こってしまうわけです。
そこでDirectXや各種GUI系では「Top-Left Filling Convention」というルールを採用しています。
② Top-Left Filling Convention(左上塗りつぶし慣習)
①にある問題を解決するために、DirectXではTop-Left Filling Convention(左上塗りつぶし慣習)というルールを敷いています。これは、「左上にあるドットは採用、右下にあるドットは不採用」というシンプルなルールです。ここで言う左上とか右下とは何なのか?
まず「左」とは三角ポリゴンの辺がポリゴンの真ん中から見て左側にある辺を言います。「右」はその逆です。「上」というのは水平な辺で真ん中より上にある辺を指します。「下」は同様にその逆です:
塗りつぶそうとしたドットが辺に相当している場合、それが左上であれば採用、右下であれば不採用とします。このルールを先程の板ポリに適用するとこうなります:
青いセルは左下のポリゴンによって塗りつぶされる箇所です。このポリゴンには左、右、下辺がありますが、このうち右辺と下辺に属しているセルは不採用です。ですから対角線の部分と最下部は色が塗られません。左上の(0,0)ドットは左辺と右辺の両方が共有しています。この場合不採用を取ります。
一方赤いセルは右上のポリゴンによる塗りつぶしセルです。これには上、左、右辺があります。右辺は不採用なので右端が塗りつぶされていません。(4,4)ドットも同様です。一方で左辺(対角線の所)は塗りつぶされます。これにより左下ポリゴンとの境界線の多重塗りつぶし問題も解決しています。矩形の大きさも設定通りの4×4です。
基本的には、このルールに従うとうまくいきます。しかし、例外もあります。
③ Top-Left Filling Conventionが適用されない場合
ところで、この慣習が適用されない場合があります。例えば以下を御覧下さい:
先ほどと同じ大きさの板ポリゴンがちょっと左上にずれています。この場合、TLFCルールを適用すると、右側が不必要に欠けてしまいます。DirectXはこういう場合にTLFCルールを適用しません。それをどこで見分けているかと言うと、上図の対角線のクロスした部分です。ここがピクセルの境目に入っていない場合など、特定の条件になっている場合、RLFCルールは使われません。
このようなうまい仕組みが働いて、見た目に矛盾のない描画が可能になっています。
④ もう一つの問題「ピクセルのずれ」
2DのHUD等を描画する時にはできればドットバイドットで描画したいものです(Dot by Dot:画面の1ドットにテクスチャの1ピクセルが描画される状態)。ところが、DirectXの見えないルールによって、意図せずにそうならない事があります。
すんごい簡単な例で再現してみます。今2×2のテクスチャがあったとしましょう。それと同じ大きさの板ポリゴンも用意します。これを下のようにスクリーンに描画するとします:
この時実際の画像はどうなるか?多分こんな感じになります:
なんだかくすんでいます。これは混色してしまったためです。なぜこんな事が起こるのでしょうか?これはテクスチャからサンプリングする際のUVが関係しています。
ラスタライズが行われると、スクリーンの有効ドットに対してUVが計算されます。具体的には各ドットの中心点(オレンジの点)に対応した値が補間計算されます。UVを書き込むとこういう感じです:
このUVにある色は上図の通りです。各UVサンプリング点が、辺上及び交点にあるのに注目して下さい。こういう場合、サンプラーの設定にもよりますが、周りの色の情報を活用して中間色が穿たれてしまいます。そのため、結果画面のように微妙に混色した色になってしまったわけです。
3Dのモデルを描画する時には、そもそもドットバイドットになることは普通ないので、こういう事に気を使う必要はほとんど無いのですが、例えばポストエフェクトをシェーダで作るときなどにはこの影響が直撃する事になります。
混色されると困るわけです。ではこれを防ぐにはどうするか?上の図に殆ど答えがあるのですが、元のポリゴンの座標を左上に0.5ずつずらします。すると、本来色を塗りたい位置とポリゴンの貼付け位置の見た目がぴったりと合います:
このUVでサンプリングすると、正確にテクスチャの色が反映されます。この元のポリゴン座標を(-0.5, -05)だけオフセットしないと理屈上ドットバイドットにならないのですから怖いもんです。
尚、これは元のポリゴン座標が整数でないと成り立ちませんので気をつけて下さい。
⑤ どこで-0.5する?
理屈は分かりましたが、ではどこで-0.5すれば良いでしょうか?板ポリゴンを座標変換済み頂点で作成している人なら、直接頂点座標をオフセットすれば終わりです。そうではなくて、板ポリを座標変換済み頂点を使わず3D空間上のポリゴンとして扱っている場合、位置をずらすチャンスは2箇所あります。
一つはワールド変換行列です。ここにスクリーンで見た時に(-0.5, -0.5)だけずれるオフセットを追加します。ただ、一般にはこれは中々難しいもんです。
もう一つはシェーダ内です。板ポリ描画用のシェーダがあるという前提ですが、WVP行列を掛けた後の頂点に対して自前で次のような計算を施します:
VS_OUT vs_main( VS_IN In ) {
VS_OUT Out = (VS_OUT)0;
Out.pos = mul( In.pos, WVPMatrix ); // 射影空間へ移動
// スクリーン座標に対して(-0.5, -0.5)のオフセット
Out.pos /= Out.pos.w;
// 射影空間の座標を一度スクリーン座標にして、
// 0.5分オフセットしてからもとに戻します。
// 下のように書いてもきっとコンパイラがうまいこと最適化してくれます(笑)
Out.pos.x = (Out.pos.x * screenW - 0.5f) / screenW;
Out.pos.y = (Out.pos.y * screenH + 0.5f) / screenH;
return Out;
}
WVPMatrix(ワールドビュー射影変換行列)をローカル座標に掛けた後に各成分をw成分で割ると、頂点座標は(-1, -1, 0) ~(1, 1, 1)という小さな領域にぎゅっと収まります。これが引き伸ばされてスクリーン座標になるわけです。今はスクリーン座標ベースで0.5のオフセットを入れたいので、一度スクリーンの幅と高さを座標に掛けてスクリーン座標に変換し、0.5のオフセットを入れて、改めてスクリーンの幅高で割って小さな領域に戻します。Y成分はスクリーンの軸と射影空間の軸の向きが逆なので足し算するのに注意です。
ドットバイドット表示は2Dの時代には当たり前(というかそれしかない)のですが、3DがベースとなっているDirectXにとっては案外難しい事がわかります。でも、ラスタライゼーションルールと頂点補間の仕組みを逆手に取れば出来そうですね。