ホーム < ゲームつくろー! < DirectX技術編
その70 完全ホワイトボックスなパースペクティブ射影変換行列
「今更何を?」という題目ではあります(^-^;。パースペクティブ射影変換行列は3Dを描画する時に間違いなく使用する行列の一つです。DirectX9の場合はD3DXMatrixPerspectiveFovLH関数を使うと自動的にそういう行列を作ってくれます。でも、な〜んとなくふわふわっとした感じで使っていませんか?また、中身の数字とか式の形を見るも「ん〜、まぁ何かやっているんだろうなぁ」と受け流してしまっていませんか?ワールド変換行列よりも実は良く分からずに使ってしまう事が多いこの行列。これって…ブラックボックスで不安な要素でもあります。
そこで本章では、パースペクティブ射影変換行列を丸裸にしてしまいます。似たような事はマルペケのあちこちに散らばっているのですが、ここにぎゅーーっと凝縮します(^-^)。
① 目に映る世界をぎゅーーっと圧縮
パースペクティブ(Perspective)というのは「遠近法」という意味です。近くの物はより大きく、遠くのものはより小さくすると遠近感が生まれます。それを3Dの世界で実現するのがパースペクティブ射影変換行列です。
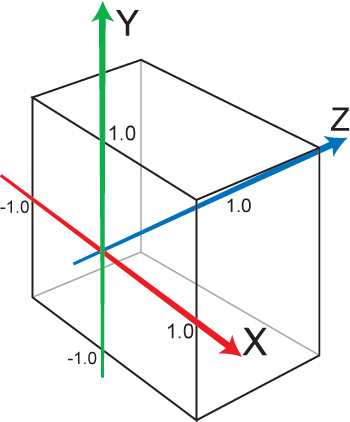
3Dの空間は広大です。フィールドの遠くに見える山々、延々と広がる海と空…。しかし、実際の「描画範囲」というのは次のような非常に小さい空間しか実は描画していないんです:
XYはそれぞれ-1.0〜1,0、奥行きであるZは0.0〜1.0。この小さな直方体の範囲に入っているポリゴンが描画対象になるんです。そのため、私達は広大な世界を構成するポリゴンをこの範囲にぎゅーーーーーっと押し縮める必要があるんです。これに正確な名前があるかはわかりませんが、区別しやすいように「描画空間」とでも名前を付けておきましょう。
ぎゅーっと押し縮めると言っても単純ではありません。例えば、山やビルや人や蟻はそれぞれ何らかの長さの基準でもってモデリングされているはずです。山なら1000m級の大きさ、人は1.7mくらい、蟻ん子なら1cmなど。それを世界に配置し、単純にすべてのモデルを等しくぎゅーっと縮めて描画空間に収めたとします。すると人は蚤くらいに小さくなりますし、蟻はもう細胞位の大きさになるかもしれません。その状態で蟻を撮影しようとしても全く見えません。なぜなら、この描画空間には「奥行き」という概念が全く無いからなんです。カメラは原点にあってZ軸方向を向いているのですが、蟻がどれだけカメラに近付いても、またどれだけ離れても同じ大きさにしか見えない世界なんです。この特殊な世界に遠近感を与えるには、世界にある物を等しく縮めるのではなくて「遠くにあるモデル程より小さく縮め、近くのモデルは殆ど縮めない」と奥行きによって意図的に縮める量を変えないといけないんです。
そこで登場するのが「視錐台」という考え方です。
② 視錐台を描画空間に変換する
視錐台というのは直方体や円柱など上面と下面がある図形の一つで、上下面の大きさが異なる図形を言います。その中で角錐台(frustum of pyramid)というのが3Dでは重要です。次のような図形です:
上下面は長方形で、Z軸方向にメガホンのように広がっています。この長方形の部分は一般にはスクリーンの縦横比と一緒になっています。メガホンはうーんと向こうまで広がっているのが普通なので、上の赤枠で示したようにどこかの奥行きでスクリーンサイズと同じ長方形があったりします。
上図は先程の描画空間と構図が一緒です。違うのは「切り取る世界の形」。この視錐台の範囲に入っているポリゴンはすべて描画対象としたいんです。でも、真の描画空間というのは①の狭い直方体の範囲でしかない。ではどうするかと言うと、上の視錐台を描画空間の形に変形するんです。そして、その変形の過程で何と遠近感が生まれてしまうんです。以下の視錐台を描画空間に変形するプロセスを見るとそれが何となくわかります。
どんな感じで変形するか、その過程を図で見てみましょう:
A. 「台」の形を1:1に
描画空間のXY平面の形は正方形でした。視錐台の「台」の部分もまずその形に変形します。
今視錐台の「台」部分はスクリーンのWidth:Heightになっています。その比率を正方形、つまり1:1になるように横方向に拡縮を行います(普通スクリーンは横長なので縮小)。どれだけ縮小するかと言うと、Height/Widthです。例えばスクリーンがW:H=2:1だとしたら、横を半分のスケールにすれば正方形になりますよね。それはH/W=1/2です。
この変形で台の形が描画空間のそれと縦横比が一致します。こうすると、赤枠の正方形のようにZ軸方向のどこかに縦と横の長さが描画空間のそれ(2,
2)と一緒になる形もあるはずです。この赤枠の大きさ、以下で重要になってきます。
B. 「台」の縦横の長さをすべて(2, 2)に
次に「台」の縦横の長さがすべて描画空間の縦横と同じ(2, 2)になるように変形します。メガホン型の視錐台をどう上図のような直方体にするか?話は簡単で、広がっている部分は狭め、狭過ぎる所は広げてあげるんです。これはある奥行きZに対してどのくらいXY平面方向に拡縮するかというお話になります。
これでXY平面については金太郎飴のようにどこを切っても描画空間と同じ大きさになりました。後Z軸方向の調整だけです。
C. -nZだけずらして(fZ-nZ)だけ縮める
先程の直方体の形から、次にZ軸の反対方向にnZだけすすすっと並行移動させます。これで手前側の台面を原点にくっつけてあげれば、後はZ軸方向にぎゅーっと縮める事で上図のように描画空間とぴったり一致するようになります。どれだけZ軸方向に縮めるかと言うと、Z軸方向の辺の長さが1になるように、つまり直方体のZ軸方向の長さ分だけ縮めます。これは先程の図から明らかで(fZ - nZ)ですよね。ですから(fZ - nZ)だけ縮小させれば見事に描画空間と同じ形になます。
こうプロセスを見て行くと、実は視錐台というのは「スケール変換と並行移動」だけで上の描画空間の形になる事がわかります。図形的な概念はなるほど納得。で、パースペクティブ変換行列というのはこのプロセスを「ほぼ」行列の中に閉じ込めているんです。この「ほぼ」という所が実は肝です。
③ A:「台」の形を1:1に(アスペクト比)
では行列のお話スタート。まず、スクリーンの縦横比になっている台の形を正方形にするようにX軸方向にスケールをかけます。横:縦=W/Hなら、かけるスケールはH/Wです。ちょうど逆数になると言う訳。これを行列で表現すると:
となります。スケール変換行列ですね。世界にあるポリゴンすべてにこの行列を適用したら、横長のスクリーンであればモデルはX軸方向に縮んでしまう事になります。でも、それによって縦横1:1をスクリーンの縦横比に戻すと元のモデルの形状が描画される事になります。
④ B:台の縦横の長さをすべて(2, 2)に(画角と奥行き依存拡縮)
次に視錐台を直方体に変形させるBのプロセスです。視錐台はZ軸(=奥行き)が大きい程その台が比例して大きくなっていくのが特徴です。視錐台を真横から眺めた下の図をご覧ください:
左の図の肌色な部分が視錐台です。真横から見ているので右方向にZ軸があります。とある奥行きzの所での視錐台の台の高さをsyとしました。今やりたい事はこのsyにスケールをかけて描画空間のと同じ高さ1にしたいんです。syに何か掛けて1にする…それは1/syを掛け算するって事です。つまり、syの値がわかればスケール値も分かると言う話になります。
視錐台の広がり具合を「画角(Angle of view)」と言います。syの値を定めるには画角を適当に決めなければなりません。例えば画角を広くすると、カメラの広角レンズと同じく広い視野範囲を捉える事ができます。逆に小さくすると今度は望遠レンズと同様で狭い範囲ですが遠くにある物もより大きく画面に映せるようになります。
今何らかの画角θを決めたとしましょう。そうすると右図にあるように画角の半分(θ/2)を持つ直角三角形からtanを使って1/syを求められます。すなわち、
と算出できます。tanは「底辺分の高さ〜」っと覚えておくと便利です(^-^)。
X軸方向のスケールは実は1/syと同じです。というのもプロセスAの所で台の形が正方形になっちゃったからです。結局このプロセスBはX,Y共に1/syだけスケール変換する、という行列になるわけです:
ところが、この行列はちょっと問題があります。行列の中に「z」という奥行きの値が入ってしまっています。θは定数ですがzはポリゴンの頂点座標など行列を適用する座標値そのものです。それが行列の中に入っていると、座標値zが変わる度に行列を作り直す必要が出てきてしまいます。それでは行列を使う意味が殆ど無いのです。
そこで、上の行列から定数部分とz部分を切り離してしまいます:
しばらくこれで様子見です(^-^;
⑤ C:-nZだけずらして(fZ-nZ)だけ縮める
最後の工程は直方体状になった視錐台のZ方向の位置を-nZだけずらして台の面を原点にくっつけ、それを(fZ-nZ)だけ縮めて描画空間とぴったり一致させる変換です。これは至って普通の並行移動とスケール変換だけで済みます:
⑥ A,B前半,Cを全部掛け算!
A,B,Cの順に変換していくと視錐台は描画空間にピッタリ一致するようになります。ただ、Bの1/zについては問題です。そこで、このスケール変換を大胆にも「しない」事にします。すると、Bの過程で視錐台は直方体にはならず、画角θの影響が取り除かれて、奥行きzの値とその時の「台」の辺の長さが2zになる、つまり画角が90度に引き伸ばされた統一的な視錐台になります:
左がプロセスAまでの段階、右がプロセスBのcot(θ/2)まで適用した段階です。高さが奥行きと同じzになっていますよね。この高さを1/z倍すれば確かに直方体になります…が、今はそれを敢えてしません。右図にさらにプロセスCの行列を適用するとZ軸方向の並行移動とスケールが入り、視錐台のZ軸方向の長さが1になります:
で、この変換をした最後の最後に1/z倍するプロセスBの後半の変換を施します。と言う事で、プロセスA,B前半,Cを掛け算してみましょう:
これが単純なパースペクティブ射影変換行列です。数値計算等で使うにはこれで十分。例えばこの行列をMp1として、
と計算すると右辺の変換後の座標が出てきます。でもこのx'とy'はまだ1/z倍されていない座標なので、
と1/z倍する事で最終的な描画空間に収まる座標を得る事が出来ます。
⑦ GPU用のパースペクティブ行列
さて、⑥のパースペクティブ行列はCPUでガリガリと計算するには事足ります。しかし、GPUを通した3D描画用として使う事は実は出来ません。理由は最後の最後「1/z倍する」という所をGPUが個別にはやってくれないためです。実は、GPUが最後の最後にやってくれる事は「変換後のx,y,z,w成分すべてをw成分で割る」なんです。なぜw成分なのでしょうか?その理由を見て行きましょう。
⑥までのプロセスの最後では変換前のz成分の値でx,y成分を割る必要がありました。つまり、どこかで変換前のz成分の値を取っておく必要があるんです。⑥までのパースペクティブ行列変換後、よ〜く見るとw成分が相変わらず「1」になっています。これが勿体無い訳です。「んじゃ、ここにz成分の値を入れておけばいいじゃん!」と考えた研究者の方々。⑥のパースペクティブ行列に細工をしたんです。それがこちら:
右下の赤文字に注目です。3行目の右端は⑥では0でした。4行目の右端は1でした。これを上のように変えたんです。行列の4列目というのはw成分の値を計算する部分です。実際(x, y, z, 1)という座標に掛け算してみると:
右の計算結果に注目!w成分に変換前のz成分の値がそのまんま出てくるでは無いですか(^-^)。これは素晴らしいとなった訳です。GPUがw成分で各成分を割るという作業をしてくれるのは、こういう細工を前提としているからなんです。
ところが、これだけだとヤバいもう一つの問題があります。上の式の右辺の各成分を実際にw成分で割ってみます:
これ、⑥の最後と良く見比べてみて下さい。z成分が違うんです。⑥の最後で導いたようにz成分は割り算してくれなくていいんです。でも、GPUは全部の成分をw成分(=z値)で割ってしまうんです。余計な事を〜〜っと思うかもしれません。確かにこのままだと余計な事なんです。
そこで研究者たちは上の行列にさらに細工をしました:
赤い部分が付けたした箇所。何をしたかと言うと、z成分を計算する所に「fZ」という視錐台の一番遠い位置のz値を付け加えたんです。この結果、右辺にあるように計算結果のz'値がfZ倍されてしまいました。しかし、これが実にうまいんです。
プロセスCで、視錐台の中にある座標のz成分は0〜1の値に収まってしまいます。上の式の右辺にあるz'の範囲がそれです。ですから、右辺のz成分の範囲は0〜fZになる事がわかります。で、最後に割るz成分の値は変換前ですからnZ〜fZの間のどれかです。もしz=nZだったら、上の式の結果はこうなります:
右辺見て下さい!z成分は綺麗に0になります。w成分にはもちろんnZの値が入りますが、0をそれで割った所で所詮0です。変換前のz成分がnZ〜fZまでだった時に、fZ・z'/zがどういう値になるのかをグラフ化したのがこちらです:
これはnZ=100、fZ=10000とした場合のw成分で割り算もした最終的な変換座標値のz値です。見事に0〜1の描画範囲に入っていますよね。ただ、変換前のz成分の値に対して対応する0〜1の値は物凄く「近いz」に集中しています。視錐台が当初切り取るのはz=100〜10000の範囲なのに、変換後のz成分は元のzが100〜1000くらいで0〜0.9まで変化してしまいます。でも、これはある意味うまい性質でもあります。
変換後のz成分の値は「深度バッファ」に穿たれます。深度バッファはポリゴンの前後関係を調べる重要なバッファです。当然ながら「カメラに近いポリゴン」ほど前後関係がおかしくなると困ります。また、カメラに近いポリゴンはガタガタ感を減らすために高解像度メッシュにっている事が多いのです。つまり、カメラにごく近い(nZに近い)所はポリゴンが細かく、深度バッファに十分な精度が要求されてしまうわけです。上のグラフのような曲線だと、z=100〜1000位のごく近い所で浮動小数点の0.0f〜0.9fまでの精度を利用出来ています。それ以上遠い所の物はポリゴンも粗いため、まぁ0.9f〜1.0fの低精度でも何とかなるだろうとなる。そういう都合に凄く良くあっているわけです。
という事で、上のfZを付け加えた行列こそが一般によく知られている(良く使われている)GPU用のパースペクティブ変換行列なんです。
この章ではパースペクティブ射影変換行列の成り立ちについて見てきました。いつもはD3DXMatrixPerspectiveFovLH関数などで何か出来て来るこの行列。でも、中身を知ればより正しくこの行列やそれに関連する情報を扱う事が出来るようになり、アプリケーションが必要とする適切なパラメータ値も判断できます。例えば視錐台の「台」の距離(nZ、fZ)をいくつにすべきか、画角(θ)を何度にしたら世界のどの範囲を切り取れるか、など。また「解像度」の違いを吸収するのにもこの行列の知識が必要になります。曖昧さを無くしてより正しく適切にパースペクティブ行列を扱って、違和感の無い描画を目指しましょう〜(^-^)