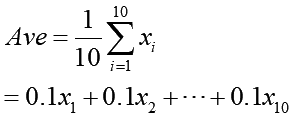
VisualStudio + Pythonでディープラーニング
平均値を求められるかな?
(2019. 12. 11)
以前の章で一つの入力値を半分にした値を返すミニマムでディープじゃないニューラルネットワークを作り、Keras的Hello
Worldを体感してみました。ここではもうちょっとだけ問題を複雑にしてニューラルネットワークに解かせてみます。解く問題は「10個の数値を入力とした時、その平均値っぽい値を出力するニューラルネットワーク」です。
① 線形回帰問題
上の平均値の問題、人間様には答えが分かっていて、次のような式で算出できます:
この式は入力されてきた個々の値に対して0.1を掛け算して全部足しています。このように「個々の値に独立に何か係数を掛け算して足す」という形になっている物を「線形回帰モデル」と言います。読んで字のごとく、上のような式はグラフに描くと直線になるから「線形」と名前が付いている訳です。「回帰」というのは変数xiが与えられた時に何らかのルールで答えが1対1で求まる式の事を言います。
ニューラルネットワークが線形回帰問題を解く事が出来る事は実は分かっています。なので表題の「平均値を求められるかな?」の問いは「Yes」です。でも試してみたいでしょ(^-^)
② 入力次元数は10、unitsは1、バイアス無しで
ではKerasでモデリングしてみます。今回の問題は平均値を求めるので10個の数値をひとまとめに扱わないと答えが出ません。よって入力値の次元数は10です。これは要素数が10の配列で設定します。それらの数値は最初の層に全部取り込まれ全部0.1倍されます。つまり重みwは一つだけで十分…なのですが、Dense層の場合全結合になるため1個1個の入力値に対して重みが対応します。なのでニューロンの数unitsは1でOKですが推定する重みの数は10個になります。入力値をオフセットするバイアスは必要ありませんので使用しないようにします。活性化関数は線形問題ですから「linear」です。この1層だけで問題は解けるので、この層がそのまま出力層になります。
以上のモデル設定をKerasに反映させてみましょう。
Kerasでのモデリングコード import keras
import numpy
#平均を取る数値の数
n = 10
#モデル作成
model = keras.Sequential()
#全結合レイヤー
#入力はn個の数値なのでinput_shapeは(1,)
#出力は1個の数値なのでunitsは1で
#バイアス(定数オフセット)は必要ない
#線形回帰問題なのでlinearで
dense1 = keras.layers.Dense( units = 1, activation='linear', use_bias=False, input_shape=(n,) )
model.add( dense1 )
#確率的勾配降下法で検索、平均二乗誤差で評価
sgd = keras.optimizers.SGD( learning_rate=0.01 )
model.compile( optimizer=sgd, loss='mse' )
#訓練開始
#10個のランダムな数値配列をn個作る -> 平均値n個算出
dataNum = 1000
train_x = numpy.random.uniform( low=-1, high=1, size=(dataNum, n) )
train_y = numpy.sum( train_x, axis=1 ) / n
model.fit( train_x, train_y, epochs=100 )
#テスト実施
testDataNum = 5
test_x = numpy.random.uniform( low=-10, high=3, size=(testDataNum, n) )
answer = numpy.sum( test_x, axis=1 ) / n
estimate = model.predict( test_x )
print( "answer: ", answer )
print( "estimate: ", estimate )
#概要表示
print( model.summary() )
print( dense1.get_weights() )
基本的な部分は以前の章で説明しているので、目新しい所をピックアップしていきます。
全連結(Dense)層の入力は10次元の配列なのでinput_shapeは(10,)というタプル指定になります。出力するのは平均値1個ですからunitsは1になります。重みは確率的勾配降下法(SDG)で最適化し、平均二乗誤差(Mean
square error)でフィッティング具合を評価します。
学習するための数値の配列をNumpyの機能を使って作っています:
#訓練開始
#10個のランダムな数値配列をn個作る -> 平均値n個算出
dataNum = 1000
train_x = numpy.random.uniform( low=-1, high=1, size=(dataNum, n) )
train_y = numpy.sum( train_x, axis=1 ) / n
model.fit( train_x, train_y, epochs=100 )
上のコードではランダムな数値10個が1まとめになった配列を1000セット作っています。numpy.random.uniformはlow~highの範囲の一様乱数を配列の要素に振る関数で、sizeには配列の型をタプルで指定します。今はC言語で言えば
train_x[ 1000 ][ 10 ] という2次元配列が欲しいのでsize=(1000, 10)と指定しています。このtrain_x[1000][10]の2次元配列が学習時の入力データとなります。
一方train_yはtrain_xにある10個の数値から求められる平均値の配列です。これが学習時の答えになります。Numpyには配列内の要素を足し合わせるsum関数が用意されているため、それを利用しています。引数axisは足し合わせる行列の方向を表していて、sizeの要素番号に相当するデータのまとまりで足し算します。axis=1としているので10個のデータを足したのが1000個分出来る事になります(train_y[1000])。で、平均なので各々の足した値をnで割り算しています。Numpyの配列は定数で掛けたり割ったり自由にできます(^-^)。そうして用意した学習入力データと答えをmodel.fit関数に食わせれば、良い感じの10個の重みが出てくるはずです。
学習後テストデータで検証しています。テストデータ(test_x)は10個の塊を5セット作って学習後のモデルに食わせています。answerには真の答え、そしてestimateにはモデルが推定した値が格納されます。
では、上のコードを実際に動かした結果をご覧ください:
Epoch 99/100
1000/1000 [==============================] - 0s 71us/step - loss: 1.5108e-13
Epoch 100/100
1000/1000 [==============================] - 0s 73us/step - loss: 1.4604e-13
answer: [-4.56394757 -2.98744353 -3.75917956 -2.54246675 -3.8966873 ]
estimate: [[-4.563949 ]
[-2.9874399]
[-3.759181 ]
[-2.5424688]
[-3.8966863]]
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 1) 10
=================================================================
Total params: 10
Trainable params: 10
Non-trainable params: 0
_________________________________________________________________
None
[array([[0.10000014],
[0.09999987],
[0.09999979],
[0.10000031],
[0.09999975],
[0.10000028],
[0.10000009],
[0.1000002 ],
[0.09999976],
[0.09999969]], dtype=float32)]
学習の結果、損失関数が返す値は十分に小さくなっています(赤い数値)。そしてテストの結果は相当に近い値になっています。一番下段には各変数にかかる重みwが表示されており、理論値0.1に大変近い値がちゃんと推定されているのがわかります!
ニューラルネットワークには「平均を求めてね」という事は一つも教えていません。でも、ちゃんと平均っぽい値を返すモデルになっている。モデルが元の式とフィットすればそういうマジックが起こるわけです。
③ 特定の数値だけ大切な重み付き平均ならどうよ?
先ほどまではすべての値に対して同じ重み0.1がかかる「算術平均」でした。これは求める答えに対する寄与の度合いが一緒という事です。これを一般化すると、各変数にかかる重みwを自由に配分しても良くなります。例えば10個の数値の内1番目と7番目だけ寄与度が3倍(0.3)だっていいわけです。実際はすべての重みを足して1になるように標準化しますが、そういう寄与度の違う平均を「重み付き平均」と言います。
先ほどのコードで学習データを作った所を少し改良して、要素番号0番の寄与度を3倍、5番のデータを4倍にた重みが違う平均値で再度学習&テストしてみましょう:
#訓練開始
#10個のランダムな数値配列をn個作る -> 重み付き平均値n個算出
dataNum = 1000
train_x = numpy.random.uniform( low=-1, high=1, size=(dataNum, n) )
weights = numpy.array([0.3, 0.1, 0.1, 0.1, 0.1, 0.4, 0.1, 0.1, 0.1, 0.1])
train_y = numpy.sum( train_x * weights, axis=1 )
model.fit( train_x, train_y, epochs=100 )
まず各要素に対応した重みwの配列(weights)を作ります。nで割る算術平均の代わりにこの重み配列を入力データに掛け算してsum関数で足すと重み付き平均(のようなもの)が出てきます。後は一緒です。で、先程と同様に学習を回しテストデータを食わせた結果がこちら:
answer: [-7.08882359 -7.57923455 -5.31120414 -4.50011149 -6.15869307]
estimate: [[-7.088815]
[-7.57923 ]
[-5.311193]
[-4.500108]
[-6.158682]]
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 1) 10
=================================================================
Total params: 10
Trainable params: 10
Non-trainable params: 0
_________________________________________________________________
None
[array([[0.2999993 ],
[0.10000006],
[0.10000015],
[0.10000009],
[0.09999996],
[0.39999893],
[0.10000016],
[0.09999997],
[0.09999995],
[0.09999994]], dtype=float32)]
5個のテストはいずれも近い値を推定してくれています。そして下段の重み配列をみると…、0番目の要素の重みがほぼ0.3、そして5番目のは0.4に非常に近い値をちゃんと推定してくれています!素晴らしいですよね。
このように線形回帰問題である場合、ニューラルネットワークは単層だけで理論値に近い値を出力する事が出来ます。では、なぜ昨今のニューラルネットワークが「ディープ(複層)」になったのか?それは、単層では解く事が出来ない問題を解決できるからです。次の章はその辺りを実験してみましょう。