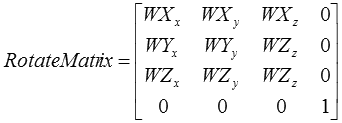
ホーム < ゲームつくろー! < DirectX技術編
その58 やっぱり欲しい回転行列⇔クォータニオン相互変換
回転行列は兎にも角にも姿勢をビシッと表すのにもっとも簡単で有効な表現方法です。具体的なお話はDirectX技術編その39「知っていると便利?ワールド変換行列が持つ情報を抜き出そう」をご覧頂きたいのですが、簡単に言うと、ローカルにあるキャラクタのX軸(1,0,0)、Y軸(0,1,0)、Z軸(0,0,1)をワールド空間でそれぞれWX=(WXx,
WXy, WXz), WY=(WYx, WYy, WYz), WZ=(WZx, WZy, WZz)という姿勢にする回転行列は、
と行列に直接書き込むと出来てしまいます。各行がキャラクタの各軸の方向そのものになっているので非常に直感的です。
直感的に姿勢を表せる回転行列(姿勢行列)には弱点があります。それは2つの姿勢行列間の補間が出来ない事です。例えば単純に、
とR1及びR2の回転行列を線形補間しても、Rotは正しい回転行列になりません。Rotが正規直交系(各行同士が直交している行列)にならないためです。
一方、姿勢を表すもう一つの方法であるクォータニオンは、たった4つの数値で姿勢を表現できます。クォータニオンの最大の強みは、行列表現で困難な「2つの姿勢の補間」が恐ろしく簡単にできてしまう点にあります。式だけ示すと次の通りです:
Q1,Q2は姿勢を表すクォータニオン、tは補間値(0~1)、そしてωは2つのクォータニオン間の角度で、クォータニオンの内積から、
と計算できます。クォータニオンの内積は、3次元ベクトル等の内積の計算と全く同じで、各要素を掛け算して足すだけです。これだけで2つの姿勢間を非常にスムーズに補間してくれるのですから素晴らしいです。
ただ、クォータニオンはその肝心の「姿勢」を回転行列のように簡単に表せません・・・と言うよりも、表現ほぼ不可能です(^-^;。キャラクタをある姿勢にしたい。でも、クォータニオンの4つの数字に何を入れたらよいか全くと言って良いほどわからないんです。直感的の真逆にいるのがクォータニオンです。
ここにすごいジレンマがあるわけです。私達は「回転行列で姿勢をビシッと定義して、しかもその間を綺麗に補間したい」という欲求がぜったいにあるんです。でも、回転行列、クォータニオン、どちらか片方だけではそれを実現できません。非情なるジレンマです。
そこでこの章では、2つの良いとこ取りをするために回転行列⇔クォータニオンの相互変換をしてみます。これができれば、2つの姿勢を回転行列で定めておいて、回転補間はクォータニオンで行い、結果として算出された補間クォータニオンをもう一度回転行列に戻す事が可能になります。尚、本章は「実例で学ぶ3D数学(オライリー・ジャパン)」を参考にしています。
① 任意軸回転行列
ジレンマを解消するための第1ステップとして、任意軸回転を表す行列を紹介します。任意軸ベクトルをn、回転角度をθとする任意軸回転行列は次のように表現される事が知られています:
この行列の出典はマルペケの参考文献でも紹介している「実例で学ぶ3D数学」です。詳細は文献を参照して頂きたいのですが、兎にも角にもこの行列を作ると任意軸で回転する行列になります。
任意軸回転というとクォータニオンの十八番で、上の任意軸回転行列と実にうまい関係があります。クォータニオンの各要素x,y,z,wでこの任意軸回転行列の各要素を表現できてしまいます。
② クォータニオン→回転行列変換
クォータニオンの各要素は回転軸ベクトルnと回転角度θを用いて次のように表現されます:
これと①の任意軸回転行列をじ~っと見ると、色々と共通項がありそうな気がしますね。実は、任意軸回転行列の各要素は、全部クォータニオンのxyzw成分で表せます。例えばm11成分は、
となります。かなりビックリですね。これをしっかり展開していくと(倍角の公式等が必要です)ちゃんとm11成分になります。色々端折りますが、クォータニオン→行列変換は次の通りです:
③ 回転行列→クォータニオン変換
②の回転行列から逆にクォータニオンのxyzwを求めれば、回転行列→クォータニオン変換ができます。一番簡単なのはw成分です。これは対角成分のm11,m22,m33を足すとわかります。実際に足してみると、
となり(θ' = θ/2です)、ここから、
とw成分を算出できます。w成分は常に正なのでこのままの式が使えます。
ちょっと面倒なのはxyz成分です。実は、例えばx成分は上の方法と同様にm11-m22-m33という計算を行うと4x2-1という形で出てきます。しかしw成分と違いx成分はsin(θ/2)であるため、±の符号が存在します。そして残念な事に、上の方法だけではプラスとマイナスのどちらになるか判断できません。とりあえず±付きの結果だけ示します:
このままではどちらの符号を使ってよいのかわかりません。そこで、回転行列の別の成分も利用します。
回転行列の対角要素(m12とm21など行列の数字が反転している関係)を見ると面白い関係があるのがわかります。例えばm12とm21を足すと2wzというのが消えて4xyとなります。逆にm12からm21を引くと、今度は2xyが消えて4wzが残ります。これらの計算をすると次のようになります:
ここから何をしたいのか?例えばm12+m21をご覧ください。この右辺を4*|x|で割ると、yが出てきます。同じようにm31+m13からはz、m23-m32からはwがそれぞれ算出できます。この時、本当のxyzwの符号と出てくる符号との関係は次の表になります:
真のyzw符号 真のxの符号 算出yzw符号 +++ + +++ - --- ++- + ++- - --+ +-+ + +-+ - -+- 以下続く・・・
算出されるyzwの符号に注目です。真のxの符号が+の時は正しく出ていますが、真のxの符号が-の場合は符号が反転しています。しかし、実はこれは問題ないんです。というのは「回転クォータニオンのQと-Qは同じ回転になる」という性質があるためです。時計の回転する長針を正面から見るか裏から見るかの違いでして、同じ回転であるのに違いありません。つまり、4*|x|さえ分かれば良いんです。そして、それはもう先の式で計算してあるではないですか(^-^)v。±の符号の「+」を採用して4*|x|を作ればいいだけです。
ここまでの情報があれば「よしゃー、変換はこれでできたぜ!」と思いたくなります。しかし、実は落とし穴がありまして、もう少し考慮が必要になります。右辺を4*|x|で割る時、xが0である可能性があるんです。例えば回転軸nが(0,1,0)とすると、|x|はあっさりと0になってしまいます。この場合、4*|x|は使えません。そこで例えば4*|y|とか4*|z|、4*|w|など他の成分を使って求める事になります。
ではどの成分を採用したら良いのか?これは「m11,m22,m33を使って求めたx,y,z,wのうち一番大きい数値が良い」とShoemakeさんとKenさんが言っているようです(Shoemake and Ken(1991), Graphics Gems 2)。最大の成分を決めたら、それで割って算出される組み合わせを用いて残りの成分を算出すれば完璧です。
というように、クォータニオン→回転行列は一意に定められるのですが、回転行列→クォータニオンはビシッと一意の式が存在しないため、Web上でなかなか紹介しにくいものがあります。結果として、回転行列→クォータニオンの情報がWeb上で希薄になっていたように思います。
④ 回転行列⇔クォータニオン変換関数+α
では、毎回恒例の関数公開です。今回は汎用性を高めるためにDirectXで定義されているベクトル変数(D3DXVECTOR3)を使っていません。と言うのも、DirectXには回転行列→クォータニオン変換をしてくれるD3DXQuaternionRotationMatrix関数がもう用意されているんです(^-^;。DirectXをお使いの方は素直にそちらを使用した方が楽です。
今回用意した関数は次の通りです:
・transformQuaternionToRotMat (クォータニオン→回転行列変換)
・transformRotMatToQuaternion (回転行列→クォータニオン変換)
・slerpQuarternion (クォータニオンによる回転補間)
・slerpRotMatDX (回転行列による回転補間(DirectX用))
・slerpRotMat (回転行列による回転補間(汎用))
| 回転行列⇔クォータニオン変換関数群 |
| /////////////////////////////////////////////// // クォータニオン→回転行列変換 // // m11-m33 : 回転行列成分(出力) // qx, qy, qz, qw : クォータニオン成分 // // ※注意: // 行列成分はDirectX形式(行方向が軸の向き)です // OpenGL形式(列方向が軸の向き)の場合は // 転置した値を格納するようにして下さい。 void transformQuaternionToRotMat( float &m11, float &m12, float &m13, float &m21, float &m22, float &m23, float &m31, float &m32, float &m33, float qx, float qy, float qz, float qw ) { m11 = 1.0f - 2.0f * qy * qy - 2.0f * qz * qz; m12 = 2.0f * qx * qy + 2.0f * qw * qz; m13 = 2.0f * qx * qz - 2.0f * qw * qy; m21 = 2.0f * qx * qy - 2.0f * qw * qz; m22 = 1.0f - 2.0f * qx * qx - 2.0f * qz * qz; m23 = 2.0f * qy * qz + 2.0f * qw * qx; m31 = 2.0f * qx * qz + 2.0f * qw * qy; m32 = 2.0f * qy * qz - 2.0f * qw * qx; m33 = 1.0f - 2.0f * qx * qx - 2.0f * qy * qy; } /////////////////////////////////////////////// // クォータニオン→回転行列変換 // // m1-m3 : 回転行列成分(出力) // q : クォータニオン成分(x,y,z,w) // // ※注意: // 行列成分はDirectX形式(行方向が軸の向き)です // OpenGL形式(列方向が軸の向き)の場合は // 転置した値を格納するようにして下さい。 void transformQuaternionToRotMat( float m1[3], float m2[3], float m3[3], const float q[4] ) { transformQuaternionToRotMat( m1[0], m1[1], m1[2], m2[0], m2[1], m2[2], m3[0], m3[1], m3[2], q[0], q[1], q[2], q[3] ); } /////////////////////////////////////////////// // クォータニオン→回転行列変換 // // m : 回転行列成分(出力) // q : クォータニオン成分(x, y, z, w) // // ※注意: // 行列成分はDirectX形式(行方向が軸の向き)です // OpenGL形式(列方向が軸の向き)の場合は // 転置した値を格納するようにして下さい。 void transformQuaternionToRotMat( float m[16], const float q[4] ) { memset( m, 0, sizeof(float) * 16 ); transformQuaternionToRotMat( m[0], m[1], m[2], m[4], m[5], m[6], m[8], m[9], m[10], q[0], q[1], q[2], q[3] ); m[15] = 1.0f; } /////////////////////////////////////////////// // 回転行列→クォータニオン変換 // // qx, qy, qz, qw : クォータニオン成分(出力) // m11-m33 : 回転行列成分 // // ※注意: // 行列成分はDirectX形式(行方向が軸の向き)です // OpenGL形式(列方向が軸の向き)の場合は // 転置した値を入れて下さい。 bool transformRotMatToQuaternion( float &qx, float &qy, float &qz, float &qw, float m11, float m12, float m13, float m21, float m22, float m23, float m31, float m32, float m33 ) { // 最大成分を検索 float elem[ 4 ]; // 0:x, 1:y, 2:z, 3:w elem[ 0 ] = m11 - m22 - m33 + 1.0f; elem[ 1 ] = -m11 + m22 - m33 + 1.0f; elem[ 2 ] = -m11 - m22 + m33 + 1.0f; elem[ 3 ] = m11 + m22 + m33 + 1.0f; unsigned biggestIndex = 0; for ( int i = 1; i < 4; i++ ) { if ( elem[i] > elem[biggestIndex] ) biggestIndex = i; } if ( elem[biggestIndex] < 0.0f ) return false; // 引数の行列に間違いあり! // 最大要素の値を算出 float *q[4] = {&qx, &qy, &qz, &qw}; float v = sqrtf( elem[biggestIndex] ) * 0.5f; *q[biggestIndex] = v; float mult = 0.25f / v; switch ( biggestIndex ) { case 0: // x *q[1] = (m12 + m21) * mult; *q[2] = (m31 + m13) * mult; *q[3] = (m23 - m32) * mult; break; case 1: // y *q[0] = (m12 + m21) * mult; *q[2] = (m23 + m32) * mult; *q[3] = (m31 - m13) * mult; break; case 2: // z *q[0] = (m31 + m13) * mult; *q[1] = (m23 + m32) * mult; *q[3] = (m12 - m21) * mult; break; case 3: // w *q[0] = (m23 - m32) * mult; *q[1] = (m31 - m13) * mult; *q[2] = (m12 - m21) * mult; break; } return true; } /////////////////////////////////////////////// // 回転行列→クォータニオン変換 // // qx, qy, qz, qw : クォータニオン成分(出力) // m1[3] : 回転行列成分 m11 - m13 // m2[3] : 回転行列成分 m21 - m23 // m3[3] : 回転行列成分 m31 - m33 // // ※注意: // 行列成分はDirectX形式(行方向が軸の向き)です // OpenGL形式(列方向が軸の向き)の場合は // 転置した値を入れて下さい。 bool transformRotMatToQuaternion( float q[4], const float m1[3], const float m2[3], const float m3[3] ) { return transformRotMatToQuaternion( q[0], q[1], q[2], q[3], m1[0], m1[1], m1[2], m2[0], m2[1], m2[2], m3[0], m3[1], m3[2] ); } //////////////////////////////////////////// // クォータニオン球面線形補間 // bool slerpQuaternion( float out[4], const float q1[4], const float q2[4], float t ) { // 角度算出 const float len1 = sqrt( q1[0] * q1[0] + q1[1] * q1[1] + q1[2] * q1[2] + q1[3] * q1[3] ); const float len2 = sqrt( q2[0] * q2[0] + q2[1] * q2[1] + q2[2] * q2[2] + q2[3] * q2[3] ); if ( len1 == 0.0f || len2 == 0.0f ) return false; // 不正なクォータニオン const float cos_val = (q1[0] * q2[0] + q1[1] * q2[1] + q1[2] * q2[2] + q1[3] * q2[3]) / (len1 * len2); const float w = acosf( cos_val ); // 球面線形補間 const float sin_w = sinf( w ); const float sin_t_w = sinf( t * w ); const float sin_inv_t_w = sinf( (1.0f - t) * w ); const float mult_q1 = sin_inv_t_w / sin_w; const float mult_q2 = sin_t_w / sin_w; for ( int i = 0; i < 4; i++ ) out[i] = mult_q1 * q1[i] + mult_q2 * q2[i]; return true; } //////////////////////////////////////////// // 回転行列による補間(DirectX専用) // // out : 補間回転行列(出力) // rm1 : 始点回転行列 // rm2 : 終点回転行列 // t : 補間値(0.0f~1.0f) D3DXMATRIX *slerpRotMatDX( D3DXMATRIX *out, const D3DXMATRIX *rm1, const D3DXMATRIX *rm2, float t ) { // 始点・終点のクォータニオンを算出 D3DXQUATERNION Q, Q1, Q2; D3DXQuaternionRotationMatrix( &Q1, rm1 ); D3DXQuaternionRotationMatrix( &Q2, rm2 ); // クォータニオン間の球面線形補間 D3DXQuaternionSlerp( &Q, &Q1, &Q2, t ); // 回転行列に戻す D3DXMatrixRotationQuaternion( out, &Q ); return out; } //////////////////////////////////////////// // 回転行列による補間(汎用) // // out : 補間回転行列(出力) // rm1 : 始点回転行列 // rm2 : 終点回転行列 // t : 補間値(0.0f~1.0f) void slerpRotMat( float out[16], const float rm1[16], const float rm2[16], float t ) { memset( out, 0, sizeof(float) * 16 ); // 始点・終点のクォータニオンを算出 float Q[4], Q1[4], Q2[4]; const float *x1 = rm1 + 0; const float *y1 = rm1 + 4; const float *z1 = rm1 + 8; const float *x2 = rm2 + 0; const float *y2 = rm2 + 4; const float *z2 = rm2 + 8; transformRotMatToQuaternion( Q1, x1, y1, z1 ); transformRotMatToQuaternion( Q2, x2, y2, z2 ); // クォータニオン間の球面線形補間 slerpQuaternion( Q, Q1, Q2, t ); // 回転行列に戻す transformQuaternionToRotMat( out, Q ); } |
ご自由にコピペしてお使い下さい。使い方はコメントをご覧ください。