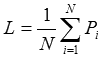
ホーム < ゲームつくろー! < DirectX技術編
その59 カメラに世界を収めるには?
ゲームを作っているとカメラに特定のキャラクタを全部収めなければならない状況が生じるときがあります。例えばアクションゲームで自分と敵群とをカメラに常に収め続ける必要があるかもしれません。その時、いったいカメラをどこまで引く、もしくはズームする必要があるのでしょうか?この章ではカメラに世界を収める方法について試行錯誤してみます。
① 世界にある2点とカメラの関係で考える
DirectXでのカメラは「位置」と「方向」、「画角」、「遠近面距離(視錐台の前後の面までの距離)」を持っています。位置と方向の情報はビュー行列に、画角と遠近面距離の情報は射影変換行列に刻印されます。通常はそれらの情報を与えて行列を作るので、実は元から持っている情報でもあります。
今世界にカメラが1台あり、また2つの点が置かれているとしましょう。この2点をカメラに収める事を考えてみます。多くの場合カメラはあらゆるアングルを向き、あらゆる位置に行く事ができるので、何らかの制約が無いと逆に難しくなってしまいます。そこで、次のような制約(プロセス)を仮定する事にします。
・ 最初にカメラのアングルが決まる
・ 次に複数の点を代表する「注視点」が決められる
・ アングルを保持したまま「位置」を動かして注視点をど真ん中に捉える
・ アングルを保持したままカメラを前後に動かして点を視錐台の中に収める
世界に2点あると、上のプロセスを最小限で考える事ができます。
② カメラのアングルを決める
カメラはあらゆる方向を向く事ができます。もしかするとキャラクタの方向を向くかもしれませんし、全然違う方向を向くのかもしれません。モデリングツールのような物を作っているのであれば軸に平行な方向を向かせる必要があるかもしれません。あらゆる方向を向けますが、その方向を向く理由があるわけです。ただ、今回の場合はこれらは全部ざっくりと「任意の方向D」としてまとめられてしまいます。
③ 複数の点を代表する注視点を決める
次に世界にある複数の点を代表する注視点を決めます。実はこれ、結構難しいんです。なんとなくぼんやりとイメージできるのは「点を全部包む境界球の中心点で良くね?」という発想です。これは全く持って正しいです。ただ、その境界球を決めるのが案外難しかったりします。これは「最小境界球問題(最小包含球問題)」と呼ばれていて、学者が論文を出す程の深い分野だったりするんです。
厳密な最小境界球を求めるのはかなりに大変です。詳しい事はEmo Weltz氏の論文
「Smallest enclosing disks (balls and ellipsoids)」
Appeared in "New Results and New Trends in Computer Science",
(H. Maurer, Ed.),Lecture Notes in Computer Science 555 (1991) 359-370.
またマルペケでも紹介している「ゲームプログラミングのためのリアルタイム衝突判定」にも上記論文を基にした記述があります。
それほど厳密性を要しない場合、あまり精度は良くないのですが全ての点の座標の平均値を求めるという簡便法があります。画面に納める点をPi、点の数をNとした時、注視点Lを次のように求めます:
簡単です。このようにして注視点を決めた後、各点と注視点間の距離を求め、最大の距離を境界球の半径と定めます。この段階で、全部の点をカメラに収めるという問題は「1つの境界球をカメラに収める」という問題になります。ざっくりしていますが、問題が簡単になる分扱いやすくなります。
④ カメラ位置を動かして注視点をど真ん中に捉える
カメラの見ている方向Dは②で既知です。また③で注視点Lも定めました。こうするとカメラのど真ん中に注視点を収めるカメラ位置を決めるのは非常に簡単になります。注視点Lからカメラの方向Dをベクトルとする直線の上であればどこでも良いんです。よって、最も簡単なのは「カメラを注視点の位置に移動させる」です。
もちろん、この状態だと境界球のど真ん中にいるので、点全体はきっとカメラに収まっていません。でもカメラの向きはわかっているのですから、後はカメラを引くだけです。
⑤ カメラを引いて境界球を視錐台内に収める
境界球のど真ん中にあるカメラを引いて境界球をカメラに収めるというのは、実は問題がかなりに簡単になっています。良く考えてみて下さい。球の中心から「どの方向に引いても」引くべき距離は同じですよね。つまり、④までで考えていた「カメラの方向」は、引く距離を計算する時には考える必要が実は無いんです。しかも、境界球の中心点の座標もどこにあっても良いわけです。
そこで、境界球の中心が原点に置いて、問題を一番簡単な状況に落とします。
後はカメラの画角を考えるだけです。DirectXの場合画角はfovY、つまりカメラの上下方向の開きで定義されます。左右方向の開きはアスペクト比から計算できます。
ここで下の図をご覧ください:
半径rの球の中心にカメラを置き、それを引いていくと、そのうち境界球と視錐台の面が接する位置がやってきます。この時の引いた距離をdとすると、図に表したような直角三角形がお目見えします。この関係はとても簡単です。斜辺がd、一辺がr、角度θの直角三角形からはsinθが次のように定義されるのでした:
sinθ=r / d
という事で、欲しい引く距離dは、
d = r / sinθ
となるわけです。θには通常fovY/2もしくはfovX/2が入ります。sinθは0~90度の範囲ならθが大きくなるほど値が小さくなるので、fovYとfovXでより小さな角度を上式に入れると引くべき距離dが判明します。
⑥ まとめ
という事で、世界(境界球)をカメラに収めるには、「半径rの境界球の中心点(注視点)Cにカメラをいったん置いて、そこからd = r / sinθ(θはfovYもしくはfovXの小さい方)だけカメラの向きと逆方向に引く」で実現できます。
⑦ 世界を収めるビュー行列を算出する関数
⑥の要素があると、世界を収めるカメラの位置(姿勢)を定められます。という事は、そこからビュー行列も簡単に求められます。そこで、そういうビュー行列を一撃で返してくれる関数を作ってみました:
世界にある境界球をカメラに収めるViwe行列を作成 ////////////////////////////////////////
// 境界球をカメラに収めるView行列算出
//
// out : ビュー行列(出力)
// r : 境界球半径
// fovY : 画角Y
// aspect : アスペクト比
// direct : カメラの向きベクトル
// up : カメラの上ベクトル
// 戻り値 : ビュー行列
D3DXMATRIX *getViewMatrixTakingSphereInCamera(
D3DXMATRIX* out,
const D3DXVECTOR3& center,
float r,
float fovY,
float aspect,
const D3DXVECTOR3& direct,
const D3DXVECTOR3& up
) {
// fovYとfovXの小さい方をθとして選択
float theta = (aspect >= 1.0f) ? fovY : fovY * aspect;
// 引く距離を算出
float d = r / sin( theta / 2.0f );
// カメラ位置確定
D3DXVECTOR3 normDirect;
D3DXVec3Normalize( &normDirect, &direct );
D3DXVECTOR3 pos = center - normDirect * d;
// ビュー行列作成
return D3DXMatrixLookAtLH( out, &pos, ¢er, &up );
}
この関数を用いたサンプルも公開致します。
この章では境界球を収める簡単な方法を紹介しました。複数のキャラクタがいる時も、それを包み込む境界球を算出すれば同様の方法でカメラに収めることができます。ざっくりですが、案外使えます。