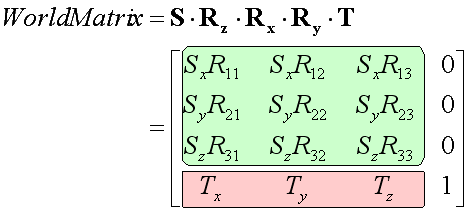
ホーム < ゲームつくろー! < DirectX技術編
その64 キャラクタの姿勢をSRTで持つ
DirectXには4×4行列を表すD3DXMATRIX構造体があります。もちろん、単なる行列として扱うこともできますが、DirectXで使う場合にはビュー、射影変換行列を除けば十中八九「姿勢」を表すために使われます。
行列によって姿勢がどう表現されるかはDirectX技術編その39「知っていると便利?ワールド変換行列が持つ情報を抜き出そう」やその60「変換行列A×BとB×Aの違いを知ろう」などに参考となる記事がありますが、もう一度おさらいすると、DirectXのワールド変換行列には姿勢の情報がしっかりと含まれています:
上のSはスケール変換行列、Rx、Ry、Rzはそれぞれ添字を軸とする回転行列(掛ける順番は変わることがあります)、Tは平行移動(オフセット)行列です。この順番で掛けると、ワールド変換行列の1行目にはX軸の方向ベクトル(SxR11, SyR12, SzR13)、2行目にはY軸、3行目にはZ軸の方向ベクトルがそれぞれ刻印されます。各軸ベクトルの長さがスケール値となります。4行目には平行移動量がそのままお目見えします。このように「SRT形式(Scale, Rotate, Translate)」は行列内に一番綺麗に情報が残ります。但し、スケールが入ったワールド変換を連続的に掛け合わせるとこの関係は崩れてしまいます。
さて、この行列形式による姿勢はDirectXが受け付ける姿勢として唯一ですし掛け算もできるので便利なのですが、この形で保持するのはちょっと扱いが良くありません。例えば3Dフィールドにいるキャラクタに対して「左上方向に進め」と命令したとして、16個ある数値のどこを変更したら良いのか直接指定は難しいです。行列形式は数学的にまとまっている分、各要素間が独立していないのが扱い難さに拍車をかけています。また一番辛いのが「補間」。2つの姿勢行列AとBがあるとして、これを例えば次のような線形補間、
で計算すると、合成行列Cは大抵「直交性」が失われてしまいます。直交性というのは上の1〜3行目に含まれているXYZ軸が直行しない状態をいいます。つまり基本軸が歪んでいるため、合成行列Cをそのまま適用するとキャラクタも歪んでしまうんです!一般にキャラクタはキーフレームアニメーションでモーションが付けられることがほとんどで、キーの間の中間姿勢は絶対に補間計算する必要があるわけで、この性質はクリティカルにヤバいわけです。
このような理由から行列形式で姿勢を管理していると不便が生じる面が出てきてしまいます。ではいったい姿勢はどう保持すべきなのか?この章ではその辺りを色々と検討してみたいと思います。
① オイラー角とクォータニオン
姿勢を表す方法は上の行列形式だけではありません。一般に姿勢を表す別の方法としては「オイラー角形式(軸回転形式)」と「クォータニオン形式」があります。これらについて簡単に整理してみます。
○ オイラー角形式
オイラー角形式は、モデルが存在している空間のXYZ軸の軸回転でキャラクタの姿勢を表す方法です。この形式の良い所は、姿勢を表すのにたった3個の角度値で済んでしまうそのコンパクトさです。行列形式だと9個(各軸のベクトル成分)が必要ですから非常にコンパクト。さらに姿勢を確定させるだけであれば実は2軸回転でも十分でして、ケチれば2個の数値で済むんです。また、多くのモデラーがこの形式での出力をサポートしているのも魅力です。さらに、この形式は補間が利きます。モデルが歪むということももちろんありません。
良い点が割と多いオイラー角形式ですが、欠点としては、特定の姿勢にビシッと合わせるのが難しい所です。例えば「飛んでいる鳥の方向に合わせてキャラクタの頭(視線)を向ける」という表現をしようと思ったら、X軸を何度回してY軸をどのくらい回すのか…。直感ではわかりません。また、先にX軸を回すのかY軸を回すのかという「順番依存」があります。X軸30度、Y軸-45度という値があっても、先にどちらの軸を回すのかで結果が変わってきます。これは地球儀上の位置を示す緯度経度そ数字が逆になったらぜんぜん違う場所になることを考えるとイメージできると思います。モデラーソフトであるSoftImage XSIではこの回転順序がデフォルトでXYZと決まっていますが、他のモデラーで同じという保証はありません(順序のルールは定まっています)。そしてもう一つ、極めて大きな欠点なのですが、この形式には「ジンバルロック」があります。
ジンバルロックというのは、例えばXYZ軸の順で回転させる時に真ん中のY軸が90度(もしくは-90度)回転してしまうと、Z軸とX軸が重なってしまい、Z軸をいくら回転させてもX軸回転と同じ事になってしまう現象を言います。これにより、Y軸を90度以外にしない限りはX軸やZ軸をどう頑張って回しても、元の座標系で見たZ軸回転が起こりません。動ける次元が1つ減ってしまうわけです。この状態から脱するにはY軸を90度以外の角度に回すしかありません。
姿勢を制御する上で、サイズコンパクトで補間が利くというのは大きな利点ですが、特定の方向に向けるのが難しいというのは扱う上ではマイナスです。ただ、FK(フォワードキネマティクス)によるモーション情報としてこれらの値がモデラーから直接入ってくるため、FKをする上ではもっとも親和性が高いかもしれません。
○ クォータニオン形式
クォータニオンというのは回転姿勢を表す数学的な手法の一つです。これについてはDirectX技術編その10「クォータニオンを学んでみよう」にまとめてあります。この形式は姿勢を4つの数値で表します。具体的には回転の軸となる方向ベクトルと、そのベクトルに対する回転角度です。つまり、クォータニオンは「任意軸回転」ができます。
この形式の良い点は2つの姿勢間を非常になめらかに補間できる所です。しかもジンバルロックが生じません。どのような姿勢からでも補間が可能で、特に「球面線形補間」という球面上を直線的に補間する事が簡単にできます。これは感覚的にも素直な補間で、クォータニオンを使わないと難しいものです(できなくはありません)。
クォータニオン形式の欠点は、姿勢を制御する数値について人の感覚がまったく利かないという点があるかなと思います。先程の鳥が飛ぶ方向に視線を向けようにも、4つの数値の意味合いが特殊過ぎて殆どどうして良いかわかりません。つまり、クォータニオンは特定の姿勢を表す方法としてはちょっと使いにくいんです。
② ゲームとしての姿勢の親和性
ゲームプログラムにおていて、行列形式、オイラー角形式そしてクォータニオン形式のどの形式で姿勢を持っておくべきか?これは明確な答えを出せない難問です。なぜなら、それぞれに一長一短があって、すべてに対応できる完全な物が無いためです。
ちょっと別の制約から考えてみます。
モデラーではモデル(ノード)のSRTを別々に制御します。直感が大切なデザイナさんに直感的でない行列を強いることはできません。SRTが別々に制御されるという事は、例えば「X軸回転はフレーム10〜30にかけてCubic補間(3次関数補間)する」というようにSRTそれぞれのパラメータの補間が異なります。こうなるとこれを行列形式に変換して補間するのは不可能になってしまいます。そのため、モデルデータにはSRTの情報を別々に出力します。となると、それを受けて実際に補間計算をするモデルクラスの姿勢制御もSRTを別々に扱わざるを得ません。
つまり、モデラーとの親和性を考えるならばSRT形式で姿勢の情報を持つのが一番しっくり来ます。ただ、SRT形式の苦手とする部分を克服する必要が出てきます。
③ SRTでLookAt
SRT形式で行く時に、SRTの「R」、つまり軸回転部分で姿勢をビシッと定める事が必要になります。姿勢を決めてくれる人の一人はモデラーです。これはとある姿勢を軸回転データとして返してくれます。ですから、モデラーの情報を使う分には問題ありません。
モデラーからの軸回転データ以外でも姿勢を決める必要はあります。例えばカメラワーク。カメラをとある位置に置き、目標にヘッドを向ける。この姿勢制御はDirectXのヘルパー関数だとD3DMatrixLookAtLH関数などで計算でき、結果が行列形式で返されます。これのSRT版があると潰しがききます。
LookAt系関数は、「自分が向くべき方向」と「空の方向」の2つを指定します。行列形式はこれで1つの行列が算出されますが、SRT形式は回転順序によって別の答えが出てきます。このパターン数は6つあります(XYZ, XZY, YXZ, YZX, ZXY, ZYX)。ただ、実用上DirectXであればZXY、SoftImage XSIはXYZなので、この辺りがあれば十分です。
例えばXYZの順での回転角度を求めてみます。
自分が向くべき方向をForwardベクトル、空の方向を"仮"Upベクトルとします。仮Upベクトルは必ずしもForwardベクトルと垂直である必要はありません(だから"仮"です)。まずForward、Upベクトルから姿勢3軸を計算します。ForwardとUpベクトルの両方に垂直なSideベクトルをFowardとUpの外積で求めます。次にSideベクトルとForwardベクトルに垂直な"真"のUpベクトルを算出します。これらベクトルは全部正規化しておきましょう。
次にXYZの順で回転行列を掛け算した合成回転行列の一般式を求めます。これは…え〜と、次の通り!
式中のCxはcos(θx)の略です。他も同様に置き換えています。この回転行列の各行が式にあるようにSide、Up、Forwardベクトルにそれぞれ対応しています。
行列のi行目j列目の要素をmijと表すことにします。
まずすぐに目につくのがm13の-Sy。つまり-sin(θy)からasin関数を使えばY軸の回転量であるθyがすぐに算出できます。ただし、asin関数は-π/2〜π/2(-90度〜90度)の範囲しか取れません。そのためθyはその範囲になります。
次にm32=SxCyとm33=CxCyに注目します。双方にCyがあるのでm32/m33を計算するとCyが約分されてSx/Cxとなり、これがtan(θx)である事がわかります。ここから、atan2関数によりθxが求まります。atan2関数は-π〜πまでの値を返します。
同様にm11とm12に注目すると両方にCyが入っているので、m12/m11からSz/Cz=tan(θz)が出てきて、すぐにθzも算出できます(-π〜π)。
気を付けたいのが、m13にある-Syが1、つまりCy = 0の時。これはY軸の回転が90度もしくは-90度の時で、m33とm11を分母とする上の計算は分母が0になるため破綻してしまいます。この場合は特殊計算が必要です。
Y軸回転が90度もしくは-90度は「ジンバルロック」状態です。ジンバルロックになるとX軸の回転とZ軸の回転は同じ事になってしまうため、X軸とZ軸回転は分離できません。そこで、Z軸回転を0度としてしまいます。そうするとSz=0及びCz=1ですから、m22はCx、m32は-Sxとなり、ここからX軸の回転角度をatan(-Sx/Cx)から求める事ができます。
これにより、軸回転で姿勢を定める事ができるようになります。
④ XSIにみられる変換行列の妙から保持すべき情報を吟味する
姿勢には明確な「親子関係」があります。子は親の空間を基準として移動や回転をします。この「親の空間を基準」と言うのは面白くて子は「親の空間をほぼ意識しない」というのが基本です。これはどういう事か?
例えば、親のX軸を2倍スケールしたとしましょう。親の世界が横にびょ〜んと伸びた状態です。この状態で、親の世界にいる子が自分の感覚(ローカル空間)でX軸方向に1だけ移動したとします。この時、絶対座標であるワールド空間での子の位置はどうなるか、行列計算してみましょう。
行列計算は(行オーダの場合)、親子関係の末えいの動きから掛け算していくのがコツです。今一番末えいの動きは「子の位置をX軸方向に1」です。子はこれで確定。次に「親のX軸スケールを2倍」が来ます。つまり行列は次のようになります:
話を簡単にしたいので2D空間にしました。CTL(子の平行移動)行列の3行目が平行移動要素で、m31にX軸+1があります。PSxL(親のX軸スケール)も同様に対角成分のm11がX軸スケール値なのでそこが2になっています。これをかけ算した結果、X軸方向の並行移動成分が「2」になっています。つまり、子は1ステップX軸方向に移動したと思っていても、親空間が2倍に伸びているので、結果としてワールド空間では2単位進んだ事になってしまうんです。
子供のワールド空間での姿勢は、上の様に自分のローカル姿勢の次に親の姿勢を掛け算することで一般的には求まります(行オーダの場合)。
この考えを踏襲すると、例えば下の左図ような姿勢になっている親子の親X軸を2倍に伸ばすと、子のワールド姿勢は右図のようになるはずです:
これは[子][親]という順でそれぞれのローカル姿勢をかけ算すると実際にこうなり、子の空間で正方形だった図形はワールド空間では右図のように歪んでしまいます。「でも、まぁこれはこういうもんだろう」と思っていました。
ところがです。SoftImage XSIで同じように親と子のローカル姿勢を設定すると、上とは違う下図のような結果になってしまいます:
最初これを確認した時は「えーー!」っと驚愕しました。どういう現象になっているかと言うと、親のX軸を2倍に伸ばすと、親空間も2倍に伸びるのですが、子の空間軸は親のスケール変換の影響だけ受けず、代わりに「子のX軸を2倍にする」というウルトラCな変換をします。これにより、子の軸の直交性が常に保たれるように成ります。その結果、子空間にあるモデルが歪んでしまう事も無くなります。
さてではこれをどうやって計算しようかというのが本題です。具体的には「子のワールド変換行列はどうなるか?」です。まず、子供は親の軸スケール倍だけ自分の空間の軸を伸縮させる事は間違いありません。つまり、親から「あなたの軸はどれだけのスケールになっていますか?」という「親スケール値」を貰う必要があります。子自体も自分の軸をスケーリングする事ももちろんありますから、子の軸スケール値は「親ワールドスケール×子ローカルスケール」となります。
次に回転ですが、これは子のローカル回転分だけ回転することになります。これはいつもと一緒です。続いて並行移動ですが、これは子のローカル並行移動値に親のスケールが加味されます。これで親空間内の子の姿勢が計算できました。これをさらに「スケールが入っていない」親の回転平行移動行列で変換すると子のワールド位置が確定します。
まぁナンノコッチャな話だと思いますので(^-^;、式で示します。以上の行列計算は次のようになります:
いや〜中々です。
このワールド変換のために姿勢のクラスが保持するべき情報は、
・ ワールドスケール値(CSL・PSWをベクトルで)
・ ワールド回転並行移動行列(CRLから右側の結果を行列形式で)
となります。回転平行移動とスケールを分離しておけば良いだけです。クラスサイズはスケール分だけサイズアップとなります。
ゲームプログラムの姿勢管理は、モデルを吐き出すモデラーの仕様を基準にしなければなりません。そうしないと、デザイナさんが付けたモーション等が正しく再生できなくなるからです。XSIをここで説明したのは、マルペケのライブラリをXSI規準にしようかなと考えているためです。他のモデラーをお使いの場合はそれに準拠した変換方法を採用して下さい。