ホーム < ゲームつくろー! < DirectX技術編
その71 深度バッファの精度って?
ポリゴンの前後関係を判断する「深度(Depth)」を格納するバッファである「深度バッファ(Depth buffer)」。このバッファは通常目にする事も触る事も出来ませんが、そこに書き込まれている深度がZテストで比較される事で3Dのモデルに「前後の関係」が与えられるため極めて重要です。
深度バッファでしばし問題になるのがその前後を判定する精度です。所詮デジタルな数値ですから無限に細かい精度で前後判定は出来ません。ポリゴンが殆ど密着しているような状態(キャラクタが着ている衣服やGUIの重ね合わせなど)の場合、本当は離れているはずなのに、精度不足から双方のポリゴンの深度が「同じ」と判定され、描画が激しくちらついてしまう事があります。いわゆる「Zファイト」と呼ばれるアーティファクトです。これを避けるには、密着しているポリゴンをちらつきが出無くなる距離まで離す必要があります。
そこで素朴な疑問が出てきます。「んじゃ、密着しているポリゴンをどれだけ離せばいいの?」と。これはデザイナさんにもたまに聞かれます。でも、その距離を決めるのは実はそう単純な話ではないんです。この章では、そんな深度バッファの精度について掘り下げてみようと思います。
① 深度バッファは「固定小数点」
言わずもがななおさらいですが、深度バッファはバックバッファのある1点に対応した深度(奥行きの距離)を保存するメモリの塊です。深度は0.0~1.0までの小数で表現され、0.0が一番手前の深度、1.0が一番奥の深度となります。これ以外の範囲にあるポリゴンは描画対象から外れます。この深度の小数点表現ですが、普段私達が使っているfloatとかdoubleなどの「浮動小数点」ではなく「固定小数点」で表現される事が多いです。
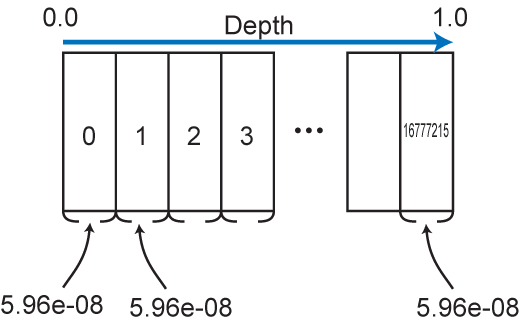
DirectXの場合、深度バッファのフォーマットにはD3DFMT_D24S8及びD3DFMT_D32が良く使われます。前者は24bit深度バッファ、後者は32bit深度バッファです。この「24bit」「32bit」というのは、固定小数点のビット幅です。例えば24bit深度バッファなら深度の0.0~1.0の間を2の24乗分割してくれます:
上図は深度バッファの分割の様子を模したものです。横方向に0.0から1.0まで深度値が大きくなっていきます。矩形は「同じ深度」とみなされる範囲で、24bit深度バッファの場合その区間距離は24bitの固定小数点なので約5.98e-08(=2^(-24))となります。この矩形は0.0~1.0の間に1667万7216個もあります(2の24乗)。
「1667万分割って十分に細かいじゃん」と思うかもしれません。しかし「パースペクティブ行列のおせっかい」を考慮すると実はそうとも言い切れないんです。
② パースペクティブ行列のおせっかい
パースペクティブ行列はモデルにワールド変換行列及びビュー行列を適用した後にさらに適用される行列で、遠近感を演出してくれる大変に重要な行列です。D3DXMatrixPerspectiveFovLH関数などで作られるあれです。そのパースペクティブ行列の典型的な例を以下に示します:
H/Wはアスペクト比の逆数、θは画角、nZとfZはそれぞれ視錐台の最近面と最遠面までの距離です。ビュー空間にあるポリゴンの頂点座標はこの行列を通す事で描画空間((-1,-1,0)~(1, 1, 1)の範囲)にぎゅーーっと縮小されます。
奥行きに関係するのはポリゴン頂点座標のz成分です。それは上の行列及び「w成分で割る」という処理で深度dに変わります。それを数式で表すと次のようになります:
実際この式で近平面までの距離であるz=nZの場合は深度dは0.0に、遠平面までの距離であるz=fZだったらdは1.0に変換されます。しかし、その間のzとdの関係は比例(線形)ではありません。むしろその変換っぷりはかなり極端でして、それが問題の本質です。下のグラフをご覧下さい:
これはnZ=100、fZ=10000とした時の各z成分値に対する深度dをプロットしたものです。横軸がz成分値、縦軸が深度です。このグラフを見ると、近平面にごく近い距離(z=100~1000くらい)の所で深度値が0.0から0.95くらいまで急上昇しているのがわかります。一方でz=1000の後は急速になだらかになっています。これはzの値が大きく変化しても深度の値が全然変化してくれない事を表しています。
zが少し変化するだけで深度が大きくかわるz=100~1000くらいの範囲なら、深度の感度が非常に良いので前後関係をかなり良い精度で判定してくれます。しかしzがそれより遠くなると極端に精度が悪くなります。それを図示したのがこちら:
横軸はビュー空間でのz成分値で、並ぶ区間はそのzでの同じ深度とみなされる範囲です。近平面近くが極端に精度が高い一方で、z=1000を過ぎるくらい辺りから精度がガクンと悪くなる様子が見て取れます。
でも「近くの精度が良くて遠くは悪い」、これはある意味都合の良い性質です。目の前の詳細なポリゴンは高精度で前後判定して欲しいし、遠くの景色は所詮遠くなのでポリゴンも粗いのが普通です。だからそもそも高精度が必要無いとも言えます。「んでは何が悪いのさ?」となりますが、その深度の区間の分布が極端なのが問題なんです。
24bit深度バッファは0.0~1.0の間を1600万以上分解する精度を持っているのですが、nZ=100、fZ=10000とした場合、z=100~1000と高々最遠の10%の距離で最初の1500万分割分くらいを消費してしまうんです。一方で残りz=1000~10000くらいの長距離範囲は100万分割くらいに激減します。長い距離を粗く分割するもんですから、その精度の落ち方がますます激しくなります。
しかも、その精度の落ちっぷりは近平面までの距離と遠平面までの距離の比が大きくなるとますます顕著になってしまうんです。では、具体的にどのくらい偏ってしまうのか?それを知るために、次に特定のz成分値にあるポリゴンの背後となれる最短の距離(最短区間距離)を求める式を導出してみましょう。
④ どれだけz座標を離せば背後になれるのか?(最短区間距離)
ちょっと数式が入ります。任意のnZ、fZをパースペクティブ行列に設定した時、あるz1に対応する深度d1は、
と計算されます。先程出てきた式そのまんまです。このz1よりも奥に位置する最短のzをz1+αと表すとすると、その深度は上の式から、
と表現できます。d1よりもdαだけ深度が奥まったというイメージですね。①にあるように24bit深度バッファはその深度差が5.96e-08よりも遠くなれば確実に前後を判定できますから、dαに5.96e-08を代入して求まるαがあるz1に対して離すべき最短区間距離となります。上のd1に最初の式を代入してαを抽出するとこうなります:
途中の計算過程はさて置き、下の式でdα=5.96e-08として求まるαがz1から離すべき最短区間距離です。式だけだと全然イメージ出来ないのでグラフ化してみます:
グラフの横軸がz成分の値(z1)、縦軸がそのz成分に対して深度差が検出できる最短区間距離dαです。パラメータはnZ=100f、fZ=10000fです。実際の数値から、z=nZ=100.0fの時は最短区間距離が5.90e-06となり、極僅かに後ろにあるポリゴンも検知できるのですが、一番遠い距離であるz=fZ=10000.0fの時は5.90e-02と実に近平面時の10000倍も離さないと前後を判定してくれなくなります!
もう少しイメージしやすいように単位をつけてみます。Z方向の1単位(z=1.0)を1mとした世界があるとしましょう。その近平面を100m先、遠平面を10km(=10000m)先に据えたとします。この時、近平面付近のポリゴンの重なりは5.90e-06m、つまり約0.006mmと非常に狭くても前後が判定されますが、500m先になると0.15mmまで下げる必要があります。1km先で0.7mm、これが5km先になると1.5cm程下げないと前後が判定されなくなります。一番遠い10km先では約6cmです。
「1km先で0.7mmなら問題無くね?」と思うかもしれません。しかし、上の例は近平面が100mと随分向こうにあり、通常のゲームで使える距離になっていません。もし近平面を1mと実用レベルの距離にし、遠平面までとの距離比を1:10000に設定するとどうなるか?こうなります:
見た目全然変わっていないように見えますが、縦軸のスケールが先程と100倍違うのに注意して下さい。ほぼ単純にどのz成分値でも先程の100倍区間を開けないと前後判定に失敗するという事です。先程500m先では0.15mmで良かった最短区間距離はその100倍の15cmに広がります。一番遠い10km先だとなんと6mも下げないといけません。
このように「前後判定の精度に非常に大きく影響するのは近平面と遠平面までの絶対距離ではなく【距離比】」なんです。
⑤ 深度の精度を体感してみよう
④であれこれ実証してみた事を試せるフォームを作ってみました。
近平面(nZ)、遠平面(fZ)までの距離を設定して、その間の任意のz成分値を与えるとその近辺の深度値と、背後として判別可能な最短区間距離を計算してくれます:
これであれこれ試してみると、24bit深度バッファの場合は近平面~遠平面の距離比はせいぜい1:1000~1:3000位がギリギリかなぁと感じます。32bitだと2桁精度が上がるとはいえ、1:10000くらいでやはり辛くなってきます。
⑥ んじゃ、どれだけ離せばいいの?
ここまでお話を踏まえて、ではモデルを作る時にどれだけポリゴンの間を離して作ればいいの?という本章の本題に踏み込んでみます。具体的な数値は深度バッファのbit数(24bitや32bit)、近平面と遠平面までの距離及びその比、そしてモデルをどの距離感で使用するかによって決まってきます。以下の数値はすべて上のフォームで算出した値を参考にしています。
近平面が1.0f、遠平面が1000.0fなちょっと狭い世界を仮定します(m単位だと思って下さい)。使うのは24bit深度バッファ。上のフォームで計算すると、遠平面の距離(z=1000)で前後判定ができる最短区間距離は0.0595fくらいでした。これがすべてのzに対応する最も大きい最短区間距離なので、これ以上広い区間でポリゴンを並べればその前後関係は世界のどこに置いても原理的には判定できる事になります。背景モデルなら保障を取って2倍の0.12fくらい離せば確実です。
広大なフィールドの地面に野草などを板ポリで並べる場合で、見えているz=200fくらいの範囲にある野草板ポリを描画対象とする(それ以上向こうのはカリングして描画しない)場合、z=200での最短区間距離は0.00238fくらいなので、保障を適度に取って0.005以上の間隔で並べればZファイトを起こさずに野草をフィールドに敷き詰める事ができます。
今度はもっと広い世界。例えば「地球上」という規模で考えてみます。キャラクタの身長が1.7m、それを追従するカメラが3m位の高さにあるとします。3mの高さから見える地平線までの距離は、地球の直径がざっくり6000kmだとして約12kmです:
z成分の1単位を1mとすると、fZは12000m。nZを1.0mにするとその比はnZ:fZ=1:12000にもなります。もし12000m先に何か大きな背景等がある場合、そこでZファイトを避けるには8.6mもポリゴンを奥へ下げる必要があります。例えば天球に雲なテクスチャを重ねる場合などこの辺りの数値を考慮しないとヤバそうですよね。そもそも、1:12000という比が厳しいかもしれませんので、fZの距離を半分の6000mに下げ、後は可能な限りnZを遠くにするよう調節します。高さ3mにカメラがあるなら、少なくとも3m以内の地面は描画範囲外になりますから、nZ=3とすればその比は1:2000まで改善します。その場合の6000m先での前後判定可能な最短区間距離は71cmにまで狭まります。
このように、具体的なワールドの広さを想定して上のフォームのような最短区間距離を計算すると、描画に不適切に起こるZファイトを未然に防いだり、起こった場合の改善策を練る事が出来ると思います。
⑦ 均等分配深度バッファは案外良いかもしれない
深度バッファ自体の精度は固定小数点(24bit及び32bit)で実は高精度です。しかし、ここまで見てきたようにパースペクティブ行列で座標を変換した段階で近平面側にバッファの精度が極端に集中してしまうため、奥行きの10%以降の距離でポリゴンの前後判定の精度が大きく落ちてしまいます。この極端な偏り、何とかならないもんでしょうか?
一つできそうだなぁと思うのが「パースペクティブ行列でz成分の変換をせず、頂点シェーダで独立して深度を求める」という方法。②の所で出てきたように、パースペクティブ行列は以下の数式でz成分値を深度に変換していたのでした:
この式中のfZ/zという所が諸問題の核となる部分。ここが反比例になっているので深度の分配が極端なんです。そこで、この計算自体を行列からごっそり省いてしまおうと発想してみます。つまり、パースペクティブ行列を次のように:
z値を計算する3列目を単位行列にしてビュー空間でのz値をそのまま採用するようにしてしまいます。この状態で頂点シェーダに突入させます。以下の頂点シェーダコードをご覧ください:
float nearZ, farZ; // 近遠平面までの距離
VSOUT vs_main( float4 pos : POSITION ) {
VSOUT Out = (VSOUT)0;
Out.pos = mul( pos, worldViewProjMat );
// 深度をここで計算(線形)
Out.pos.z = (Out.pos.z - nearZ) / ( farZ - nearZ );
Out.pos.z *= Out.pos.w;
return Out;
}
頂点シェーダ内で座標を行列変換した後、さらに深度計算を自前でやっています。計算式は最初の行列変換で算出されるz成分値(ここではビュー空間でのz成分値と等しい)からnearZを引き算し、それを(farZ - nearZ)でぎゅーっと縮めています。この変換イメージは前章を参照下さい。このように深度を計算すると、nZ~fZが0.0~1.0に線形に変換されます。次にw成分を掛けているのは、retrunで頂点シェーダから座標を出力した後勝手に全部の要素がw成分で割り算される、その効果を相殺するためです。実際の深度は1行目の計算結果そのものとなります。
このようにz値と深度を線形にした時の最短区間距離を④と同じように計算してみます。深度の計算式は上のシェーダ内にあるように:
です。シンプルですね。前後判別が可能となる最短区間距離をα、その時の差分深度をdαとすると、
で、先の式を代入してαを抽出するとこうなります:
ま~シンプル(^-^)。そして式の中にz1が無い事に注目です。これはz成分がどの値でも最短区間距離が右辺のように一定である事を表しています。24bit深度バッファの場合dαは2^(-24)ですから、nZ=1.0f、fZ=10000.0fくらいの比にするとαはおよそ5.96e-04(0.000596)となります。僕は「これ、割といいんじゃね?」と感じます。
ただ上のシェーダはちょっと不満。頂点シェーダにnearZやfarZを渡すのがメンドクサイです。そこで、パースペクティブ射影変換行列を次のようにします:
z成分を計算する所にスケールとオフセットが入りました。これは先程の頂点シェーダ内の深度計算の1行目を担っています。ですから頂点シェーダの中は、
VSOUT vs_main( float4 pos : POSITION ) {
VSOUT Out = (VSOUT)0;
Out.pos = mul( pos, worldViewProjMat );
// z成分をそのまま深度とする(線形)
Out.pos.z *= Out.pos.w;
return Out;
}
このように深度計算の1行目が無くなり、とってもシンプルになります。
頂点シェーダで直接w成分を掛け算しているので、この均等分配深度バッファを使う時にはシェーダを書き変えないといけませんが、特にシェーダ定数を追加する事は無いので既存のシェーダを改変するのも難しくは無いと思います。
では通常のパースペクティブ行列のと線形のとで前後判定可能な最短区間距離の精度を比較してみましょう:
横軸はz値です。nZ=1.0f、fZ=1000.0fとしました。縦軸はそのzで前後を判定できる最短区間距離(α)です。実数軸だとあまりに違い過ぎて読み取れないので対数軸にしてあります。1メモリ違うと精度が10倍違う事を意味しています。グラフの下の方ほど前後判定の精度が良い事を表しています。これを見るともう一目瞭然ですよね。通常のパースペクティブ行列の方は近平面から極違い所では線形よりも1~1000倍精度が良いのですが、少し距離が離れた所では精度が大きく逆転しています。
線形の最短区間距離はすべてのz値で0.0001fを少し下回るくらいになっていますが、これは1kmな奥行きの世界で0.1mmの前後を判定できる精度です。正直十分だと思います。むしろ、その精度を遠平面まで保っているのが嬉しい性質に思います。ただ、上の線形のグラフをよ~く見てもらうと、z=500あたり以降からちょっとだけ数値が上がっています。これはfloat型の精度の限界によってz=500あたりから遠い所では理想の精度で差(引き算)が出無くなるためです。それでもほんの僅かですから実用上はまったく問題ありません。
nZ:fZ=1:1000だとちょっと狭いので、nZ=1.0f、fZ=10000.0fの場合がこちら:
パースペクティブ行列(通常)の方は近い所で大変精度が高いのがわかりますが、それはわずかz=200の所で線形と逆転されます。線形の方は先程よりも全体の精度が10倍落ちます。z=1.0fを1mとすると1mm程ポリゴンを離す必要があります。ハイポリなモデルでポリゴンが1mm単位で物凄く細かく重なっている所があれば、Zファイトが起きてしまうかもしれませんが、10kmスケールな世界ですから、そういうモデルは稀かなと思います。
この章では深度バッファの精度についてあれこれ考えてきました。目に見えないけども微妙に厄介な性質を持っている深度バッファ。その仕組みを知ればZファイトを回避したりワールドの大きさを最適に決めたり、パースペクティブの近遠平面への距離比を検討したりできます。どうしてもとなれば均等分配深度バッファも使えます。ややこしいけど大切な深度。上手に付き合いたいもんですね(^-^)